A relativitási elméletek
A relativitási elméletek
@vaskalapos (16562): Le tudnad irni nekem mi a "reszecske" es a "targy" kozott a kulonbseg?
Ha valóban nem tudod, akkor minek írsz "az mind sotet ostobasag volt." ilyeneket?
Ha valóban nem tudod, akkor minek írsz "az mind sotet ostobasag volt." ilyeneket?
0 x
A relativitási elméletek
@Gézoo (16570): Talán mert nem érti amit írsz. Vaskalapos, alagi, én azt értjük amit tanultuk, és azt értjük, hogy amit te írsz az köszönő viszonyban sincs a tanultakkal. Teljesen alternatív fizikád van, ami ugyan tele van önellentmondással, értelmezhetetlen fogalmakkal, illogikus de legalább más, alternatív.
0 x
A relativitási elméletek
@Gábor (16590): Nos, ez nem meglepő. A napokban olvastam újra Einstein áltreljét három változatban. Einstein saját írását, Max Born és Wolfgang Pauli féle változatokat. Nagyon érdekes ahogyan hárman értelmezik ugyanazt.
Miközben a klasszikus hiba mindháromban benne van v=g*l/c majd ebből
f'=f*(1-gl/c2)
Amiben csak az az apró hiba, hogy ugye mi úgy tanultuk, hogy E=m*g*h .. azaz m tömegnek h magasságra emeléséhez g gravitációs gyorsulású mezőben E energiára van szükség. (Miután F=m*g és E=F*s.. azaz ez esetben E=F*h)
Csak van egy kis bibi ezzel.. mégpedig az, hogy g értéke függ a magasságtól.
Azaz h magasságon már nem g=k*M/R2, hanem gh=k*M/(R+h)2 és tetejében nem lineáris (a négyzetes hányados miatt) az erő magasság-függvénye.
Mekkora ez az eltérés? Á, nem nagy 1 kg, és 1 m magasságnál csak E=1,5 mg*g*1 [J]
Persze 10 000 méteren és 100 000 kg esetében már sok-sok szorosa..
Hogy ezt előttem senki nem vette észre? Azt kétlem. De hogy nem publikálták közismert fórumon az nyilvánvaló, hiszen ti sem tudtátok eddig.
Ettől és a hasonló felismerésektől alternatív lennék? Na az lehet.
Na az lehet.
Viszont nyilvánvalóan nem az én hibám az, hogy majdnem minden közhasználatos tétel itt-ott pontatlan megfogalmazású, inkorrekt levezetésekkel született, hanem az eredetieik elkövetőinek a hibája.
Persze azt már boncolgathatnánk, hogy ha én észrevettem, és kijavítottam, akkor mondjuk az 1916 óta Nobel dijat átvevő fizikusaink, hogy-hogy nem vették észre..?
 Ha már a többi fizikusi fizetésből éldegélő nem látta meg az alapvető hibákat, legalább a csúcs-Nobel-kés fizikusoknak látnia kellett volna.
Ha már a többi fizikusi fizetésből éldegélő nem látta meg az alapvető hibákat, legalább a csúcs-Nobel-kés fizikusoknak látnia kellett volna.
Miközben a klasszikus hiba mindháromban benne van v=g*l/c majd ebből
f'=f*(1-gl/c2)
Amiben csak az az apró hiba, hogy ugye mi úgy tanultuk, hogy E=m*g*h .. azaz m tömegnek h magasságra emeléséhez g gravitációs gyorsulású mezőben E energiára van szükség. (Miután F=m*g és E=F*s.. azaz ez esetben E=F*h)
Csak van egy kis bibi ezzel.. mégpedig az, hogy g értéke függ a magasságtól.
Azaz h magasságon már nem g=k*M/R2, hanem gh=k*M/(R+h)2 és tetejében nem lineáris (a négyzetes hányados miatt) az erő magasság-függvénye.
Mekkora ez az eltérés? Á, nem nagy 1 kg, és 1 m magasságnál csak E=1,5 mg*g*1 [J]
Persze 10 000 méteren és 100 000 kg esetében már sok-sok szorosa..
Hogy ezt előttem senki nem vette észre? Azt kétlem. De hogy nem publikálták közismert fórumon az nyilvánvaló, hiszen ti sem tudtátok eddig.
Ettől és a hasonló felismerésektől alternatív lennék?
Viszont nyilvánvalóan nem az én hibám az, hogy majdnem minden közhasználatos tétel itt-ott pontatlan megfogalmazású, inkorrekt levezetésekkel született, hanem az eredetieik elkövetőinek a hibája.
Persze azt már boncolgathatnánk, hogy ha én észrevettem, és kijavítottam, akkor mondjuk az 1916 óta Nobel dijat átvevő fizikusaink, hogy-hogy nem vették észre..?
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16570):
Erra gondolok, hogy mast ertesz ezek alatta szavak alatt is, mint amit az emberek tobbsege.
Szeretnem megerteni, hogy ha en azt mondom, hogy erohatas alatt levo targy semmit nem mond a mozgasarol (meg az sem, ha nincs erohatas alatt), akkor miert nem erre valaszolsz (egyetertesz, vagy cafolni probalsz), miert reszecskerol kerdezel?
Azert kerdeztem, mert en erohatas alatt allo targyrol irok, es te valszodban reszecsket akarsz mutattatni.Ha valóban nem tudod, akkor minek írsz "az mind sotet ostobasag volt." ilyeneket?Le tudnad irni nekem mi a "reszecske" es a "targy" kozott a kulonbseg?
Erra gondolok, hogy mast ertesz ezek alatta szavak alatt is, mint amit az emberek tobbsege.
Szeretnem megerteni, hogy ha en azt mondom, hogy erohatas alatt levo targy semmit nem mond a mozgasarol (meg az sem, ha nincs erohatas alatt), akkor miert nem erre valaszolsz (egyetertesz, vagy cafolni probalsz), miert reszecskerol kerdezel?
0 x
A relativitási elméletek
@vaskalapos (16592): Ajajjjj.. Nem tudtad?
Minden tárgy részecskékből áll! Mégpedig erőhatás alatt álló mozgó részecskékből!
Minden tárgy részecskékből áll! Mégpedig erőhatás alatt álló mozgó részecskékből!
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16591):
Tipikusan arrol van szo, hogy csak a kepletet nezed es nem olvasod el, hogy mikor, mi az aminek a leirasara hasznaljak.
Figyeld, mit irtal:
Peldaul, ha emeles kozben hullik a homok zsakodbol es igy m valtozik, akkor sem jo a keplet.
Ha valamelyik tag valtozik, akkor a keplet nem ervenyes, akkor egy kiegeszitett, korrigalt valtozatra van szukseg.
Ez nem relativitaselmelet, ez jozan esz.
Tipikusan arrol van szo, hogy csak a kepletet nezed es nem olvasod el, hogy mikor, mi az aminek a leirasara hasznaljak.
Figyeld, mit irtal:
Az E=m*g*h allando g eseten ervenyes. Ez termeszetes, nem? Mint ahogy csak allando m es allado h eseten ervenyes a keplet.az az apró hiba, hogy ugye mi úgy tanultuk, hogy E=m*g*h .. azaz m tömegnek h magasságra emeléséhez g gravitációs gyorsulású mezőben E energiára van szükség. (Miután F=m*g és E=F*s.. azaz ez esetben E=F*h)
Csak van egy kis bibi ezzel.. mégpedig az, hogy g értéke függ a magasságtól.
Peldaul, ha emeles kozben hullik a homok zsakodbol es igy m valtozik, akkor sem jo a keplet.
Ha valamelyik tag valtozik, akkor a keplet nem ervenyes, akkor egy kiegeszitett, korrigalt valtozatra van szukseg.
Ez nem relativitaselmelet, ez jozan esz.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16594):
Ennek ellenere egy targy mozoghat, vagy mozdulatlan lehet egy masik targyhoz kepest.
Es?Ajajjjj.. Nem tudtad?
Minden tárgy részecskékből áll! Mégpedig erőhatás alatt álló mozgó részecskékből!
Ennek ellenere egy targy mozoghat, vagy mozdulatlan lehet egy masik targyhoz kepest.
0 x
A relativitási elméletek
@vaskalapos (16596): "
Az E=m*g*h allando g eseten ervenyes. " Naná, de ezt sem Einstrein, sem Born, sem Pauli nem vette figyelembe.. ott virít a rossz alak az áltrelben
ott virít a rossz alak az áltrelben 
Es?
Ennek ellenere egy targy mozoghat, vagy mozdulatlan lehet egy masik targyhoz kepest.
 Ja igen. mozdulatlannak látszódhat.. de ettől még nem lesz mozdulatlan is.
Ja igen. mozdulatlannak látszódhat.. de ettől még nem lesz mozdulatlan is. 
Az E=m*g*h allando g eseten ervenyes. " Naná, de ezt sem Einstrein, sem Born, sem Pauli nem vette figyelembe..
Es?
Ennek ellenere egy targy mozoghat, vagy mozdulatlan lehet egy masik targyhoz kepest.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16598):
Idezd, a szovegkornyezettel egyutt.Az E=m*g*h allando g eseten ervenyes. " Naná, de ezt sem Einstrein, sem Born, sem Pauli nem vette figyelembe..ott virít a rossz alak az áltrelben

0 x
A relativitási elméletek
@Gézoo (16591):
A) Egy ilyen (meg szerinted is nagyon konnyen eszreveheto) dolgot mar szaz eve egyetlen fizikus sem vesz eszre, es ezert az egesz fizika rossz (De akkor miert mukodik a GPS?). Es akkor josz es forradalmat csinalsz egy ilyen kis sz*rsaggal, amivel egyedul a te intellektusod tud megbirkozni
B) Ez a tema annyira trivialis egy gyakorlo fizikusnak, hogy meg csak meg sem emliti az ilyen alapveto reszletkerdeseket. Te viszont mint Dr. Bubo es Mekk Elek, semmihez sem ertesz, csak azt hiszed hogy.
A Pertrubacio szamitas temakornel lehetne elkezdened utananezni hogy mirol is van itt szo valojaban, de az eddigi forumos palyafutasod alapjan szerintem neked felesleges ebbe belefogni.
Ez az egyetlen fatalis hiba a gondolkodasodban teljesen lehetetlenne teszi, hogy barmikor is a jovoben egyetlen ertelmes gondolatod legyen.
Felvazolom hogyan gondolkozik Gezoo, es hogyan gondolkozik egy ertelmes ember.
Az ember olvas vagy gondolkozik, es rajon egy allitasra amit "A"-val jelolok. felut egy konyvet (vagy egy wikipediat), es eszreveszi, hogy ott nem "A" szerepel, hanem "nem A" vagy valami mas "B".
Mit gondol ilyenkor egy ertelmes ember:
"Hogyaza, valamit elszurhattam. Igen, sejtettem hogy valami nem lesz jo, mert ha "A" igaz lenne, akkor az csak ugy lehet hogy az utobbi 100 evben minden kiserletet elrontottak, es direkt hibas adatokat kozoltek, az egesz tudos tarsadalom egy hatalmas osszeeskuves. Hat ez nem tul valoszinu, inkabb nezzuk csak meg a gondolatmenetemet, hol is tevedhettem?"
Mindannyiunkal megesett mar ez, es valoban, neha nem konnyu a hibat megtalalni. Sot neha az is elofordul, hogy a konyvben tenyleg hiba van. Azonban a legtobb esetben a hiba kijavithato ugy, hogy a konyv (vagy erveles) egesze nem bukik (pl. mert ok is a helyes eredmenyt hasznaljak a kesobbiekben).
Mit gondol ilyenkor Gezoo:
"Aha szoval a konyvbe hulyeseg van. nyilvanvalo, hiszen most gondoltam at, es en nem tevedhetek sohasem, tehat nyilvan mindenki mas teved. Es ezek szerint akkor az egesz "X" tudomanyag ugy hulyeseg ahogy van, a tankonyvek 3. oldalatol kezdve. Ezek a rohadt tudosok direkt olyan hamis adatokat publikalnak, hogy ugy tunjon megis igaz, valamint nehogy kideruljon en milyen okos vagyok. Mondjuk ez nem meglepetes, mert barmilyen tudomanyra nezek ra, mind hemzseg az olyan hibaktol amikre en 1 perc alatt rajovok. (Csak vegre megertene legalabb egyvalaki, hogy en milyen okos vagyok, de sajnos az egesz vilag direkt ellenem van.)"
Gezoo, szerinted melyik az igaz?Persze azt már boncolgathatnánk, hogy ha én észrevettem, és kijavítottam, akkor mondjuk az 1916 óta Nobel dijat átvevő fizikusaink, hogy-hogy nem vették észre..?
A) Egy ilyen (meg szerinted is nagyon konnyen eszreveheto) dolgot mar szaz eve egyetlen fizikus sem vesz eszre, es ezert az egesz fizika rossz (De akkor miert mukodik a GPS?). Es akkor josz es forradalmat csinalsz egy ilyen kis sz*rsaggal, amivel egyedul a te intellektusod tud megbirkozni
B) Ez a tema annyira trivialis egy gyakorlo fizikusnak, hogy meg csak meg sem emliti az ilyen alapveto reszletkerdeseket. Te viszont mint Dr. Bubo es Mekk Elek, semmihez sem ertesz, csak azt hiszed hogy.
A Pertrubacio szamitas temakornel lehetne elkezdened utananezni hogy mirol is van itt szo valojaban, de az eddigi forumos palyafutasod alapjan szerintem neked felesleges ebbe belefogni.
Ez az egyetlen fatalis hiba a gondolkodasodban teljesen lehetetlenne teszi, hogy barmikor is a jovoben egyetlen ertelmes gondolatod legyen.
Felvazolom hogyan gondolkozik Gezoo, es hogyan gondolkozik egy ertelmes ember.
Az ember olvas vagy gondolkozik, es rajon egy allitasra amit "A"-val jelolok. felut egy konyvet (vagy egy wikipediat), es eszreveszi, hogy ott nem "A" szerepel, hanem "nem A" vagy valami mas "B".
Mit gondol ilyenkor egy ertelmes ember:
"Hogyaza, valamit elszurhattam. Igen, sejtettem hogy valami nem lesz jo, mert ha "A" igaz lenne, akkor az csak ugy lehet hogy az utobbi 100 evben minden kiserletet elrontottak, es direkt hibas adatokat kozoltek, az egesz tudos tarsadalom egy hatalmas osszeeskuves. Hat ez nem tul valoszinu, inkabb nezzuk csak meg a gondolatmenetemet, hol is tevedhettem?"
Mindannyiunkal megesett mar ez, es valoban, neha nem konnyu a hibat megtalalni. Sot neha az is elofordul, hogy a konyvben tenyleg hiba van. Azonban a legtobb esetben a hiba kijavithato ugy, hogy a konyv (vagy erveles) egesze nem bukik (pl. mert ok is a helyes eredmenyt hasznaljak a kesobbiekben).
Mit gondol ilyenkor Gezoo:
"Aha szoval a konyvbe hulyeseg van. nyilvanvalo, hiszen most gondoltam at, es en nem tevedhetek sohasem, tehat nyilvan mindenki mas teved. Es ezek szerint akkor az egesz "X" tudomanyag ugy hulyeseg ahogy van, a tankonyvek 3. oldalatol kezdve. Ezek a rohadt tudosok direkt olyan hamis adatokat publikalnak, hogy ugy tunjon megis igaz, valamint nehogy kideruljon en milyen okos vagyok. Mondjuk ez nem meglepetes, mert barmilyen tudomanyra nezek ra, mind hemzseg az olyan hibaktol amikre en 1 perc alatt rajovok. (Csak vegre megertene legalabb egyvalaki, hogy en milyen okos vagyok, de sajnos az egesz vilag direkt ellenem van.)"
0 x
A relativitási elméletek
@alagi (16605): Gezoo, szerinted melyik az igaz? 1. Az igaz, hogy Alalgi úr már megint személyeskedik..
Basszushangú kisleány! Vitasd a gravitációs térerősség függvényét, ha nem értesz egyet Galilei pajtással..
De engemet ne cseszegess miatta. Főleg akkor ne, ha annyira fű vagy a témához, hogy nálad a perdületben és a lendületben tárolt energia összege nem egyenlő a mozgásokat létrehozó testtől átvett energiával.
Basszushangú kisleány! Vitasd a gravitációs térerősség függvényét, ha nem értesz egyet Galilei pajtással..
De engemet ne cseszegess miatta. Főleg akkor ne, ha annyira fű vagy a témához, hogy nálad a perdületben és a lendületben tárolt energia összege nem egyenlő a mozgásokat létrehozó testtől átvett energiával.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16603):
Most olvassak el 159 oldalt, hogy megtalaljam, mit nem ertesz?
Oldalszam?
Kerlek idezd, ne egy google kereset valaszolj.
Amugy szerintem te nem erted a szoveget csak a kepeket (kepleteket) nezegeted ezekben a konyvekben.
A helyedben valami konnyebb olvasmannyal kezdenem, es csak ha azt mar ertem, akkor vennem elo ujra ezeket a konyveket.
Most olvassak el 159 oldalt, hogy megtalaljam, mit nem ertesz?
Oldalszam?
Kerlek idezd, ne egy google kereset valaszolj.
Amugy szerintem te nem erted a szoveget csak a kepeket (kepleteket) nezegeted ezekben a konyvekben.
A helyedben valami konnyebb olvasmannyal kezdenem, es csak ha azt mar ertem, akkor vennem elo ujra ezeket a konyveket.
0 x
A relativitási elméletek
@vaskalapos (16611): Ha észrevetted pdf.. és már idéztem.. A szöveget elolvashatod, oda mutat a link, de ne várd, hogy azt is begépeljem..
Egyébként hogyan vitázhatnál ha nem ismered az áltrelt? Azaz legalább egyszer már elolvastad végig.. Vagy nem?
És különben is a nagy víz túloldalán milyen nyelven beszélnek ott ahol vagy? Csak nem anlishúúúl?
Egyébként hogyan vitázhatnál ha nem ismered az áltrelt? Azaz legalább egyszer már elolvastad végig.. Vagy nem?
És különben is a nagy víz túloldalán milyen nyelven beszélnek ott ahol vagy? Csak nem anlishúúúl?
A hozzászólást 1 alkalommal szerkesztették, utoljára Gézoo 2011.04.11. 14:44-kor.
0 x
A relativitási elméletek
@Gézoo (16607):
Nem latom ertelmet n+1-edszerre pontosan elmagyarazni hogy hol tevedsz, mert az elso n alkalommal se ertetted meg.
De egyebkent ott van az utalas ra, es barmelyik kollegam ennyibol mar ertene mire gondolok. Ez nem meglepetes, mert mar az en utalasom nelkul is ertene mindenki hogy miert mukodik az eredeti erveles.
(Azert, mert ha kelloen kis helyen vizsgalod a gravitaciot, akkor elhanyagolhato a g terfuggese. Ez a perturbacio szamitas nulladik rendje. Jol kidolgozott modszer letezik arra, hogy hogyan vegyuk figyelembe a nem konstans g-t. ha eppen az erdekel minket: ezt hivjak perturbacioszamitasnak. A konyvben levo erveles (talan impliciten) azt mondja, hogy ezek a korrekciok nem lenyegesek a vizsgalt jelenseg szempontjabol. Na, akkor megis csak elmagyaraztam )
)

Azert teged cseszegetlek, mert te allitasz hulyesegeket, es szeretnem megerteni, hogy mukodik belulrol egy ilyen (teljesen elborult) elme.
Nagyon erdekes hogy inkabb a vilagmeretu osszeeskuvesben hiszel, amiben gyakorlatilag rajtad kivul _mindenki_ benne van, csak ne kelljen a valosaggal megbirkozni. "Fascinating", ahogy Spock mondana.
(Ja igen, es szerintem az a szemelyeskedes, ha pl. valakit "Basszushangu kisleany"-nak hivsz, anelkul hogy erre barmi indokod lenne. Az eddigi hozzaszolasaim alapjan se azt nem tudhatod hogy fiu vagyok-e vagy lany, se azt hogy a korusban melyik szolamot szoktam enekelni)
Nem latom ertelmet n+1-edszerre pontosan elmagyarazni hogy hol tevedsz, mert az elso n alkalommal se ertetted meg.
De egyebkent ott van az utalas ra, es barmelyik kollegam ennyibol mar ertene mire gondolok. Ez nem meglepetes, mert mar az en utalasom nelkul is ertene mindenki hogy miert mukodik az eredeti erveles.
(Azert, mert ha kelloen kis helyen vizsgalod a gravitaciot, akkor elhanyagolhato a g terfuggese. Ez a perturbacio szamitas nulladik rendje. Jol kidolgozott modszer letezik arra, hogy hogyan vegyuk figyelembe a nem konstans g-t. ha eppen az erdekel minket: ezt hivjak perturbacioszamitasnak. A konyvben levo erveles (talan impliciten) azt mondja, hogy ezek a korrekciok nem lenyegesek a vizsgalt jelenseg szempontjabol. Na, akkor megis csak elmagyaraztam
Most itt megint van egy problema. Vagy annyira nem erted hogy mit mondok hogy egy teljesen mas ertelmu allitast adsz a szamba, vagy hazudozol. Melyik a jobb?De engemet ne cseszegess miatta. Főleg akkor ne, ha annyira fű vagy a témához, hogy nálad
Azert teged cseszegetlek, mert te allitasz hulyesegeket, es szeretnem megerteni, hogy mukodik belulrol egy ilyen (teljesen elborult) elme.
Nagyon erdekes hogy inkabb a vilagmeretu osszeeskuvesben hiszel, amiben gyakorlatilag rajtad kivul _mindenki_ benne van, csak ne kelljen a valosaggal megbirkozni. "Fascinating", ahogy Spock mondana.
(Ja igen, es szerintem az a szemelyeskedes, ha pl. valakit "Basszushangu kisleany"-nak hivsz, anelkul hogy erre barmi indokod lenne. Az eddigi hozzaszolasaim alapjan se azt nem tudhatod hogy fiu vagyok-e vagy lany, se azt hogy a korusban melyik szolamot szoktam enekelni)
A hozzászólást 1 alkalommal szerkesztették, utoljára alagi 2011.04.11. 14:49-kor.
0 x
A relativitási elméletek
@alagi (16614): Nem latom ertelmet n+1-edszerre pontosan elmagyarazni
Pontosítsunk! Ahol n=-1.. Még egyetlen épkézláb levezetést sem írtál. A személyeskedéseidről ne hidd, hogy értelmes "magyarázatok" Mert nem azok.
Mert nem azok.
Még csak értelem sem volt bennük.
Pontosítsunk! Ahol n=-1.. Még egyetlen épkézláb levezetést sem írtál. A személyeskedéseidről ne hidd, hogy értelmes "magyarázatok"
Még csak értelem sem volt bennük.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16603):
OK, most latom, az elso linked eseten a 352 oldal a (100) keplet utani masodik bekezdesben olvashatod:
This is the case for a constant gravitational filed such as occurs at the immediate surface of a celestial body.
Igy mar erted? Elore leirtak, hogy a keplet, amit kritizalsz, az allando gravitacios terre, allando g-re igaz, peldaul egy egitest kozvetlen felszinen (es nem attol messzire tavolodva).
Orulok, hogy segithettem. Ugye igy mar erted?
Sokszor elofordult mar, hogy ilyen olvasasi hiba miatt nem ertesz, felreertesz allitasokat (last pontszeru test vs forgatonyomatek).
OK, most latom, az elso linked eseten a 352 oldal a (100) keplet utani masodik bekezdesben olvashatod:
This is the case for a constant gravitational filed such as occurs at the immediate surface of a celestial body.
Igy mar erted? Elore leirtak, hogy a keplet, amit kritizalsz, az allando gravitacios terre, allando g-re igaz, peldaul egy egitest kozvetlen felszinen (es nem attol messzire tavolodva).
Orulok, hogy segithettem. Ugye igy mar erted?
Sokszor elofordult mar, hogy ilyen olvasasi hiba miatt nem ertesz, felreertesz allitasokat (last pontszeru test vs forgatonyomatek).
0 x
A relativitási elméletek
@vaskalapos (16617): Pici szívecske! Erről írtam: This is the case for a constant gravitational filed such as occurs at the immediate surface of a celestial body. Nem állandó.. Már egyetlen méteren sem állandó.. Sőt mikron távolságon sem állandó.. Érted? Mégis úgy szerepel a függvényekben, mintha állandó lenne és nem a fentebb leírt alakban.
persze ha a differenciálokkal írta volna fel.. és természetesen nem csak utalva a rel. Doppleres helyes alakra, hanem behelyettesítve.. akkor egy szavam sem lehetne.
DE mint olvasható mindhárom műben.. nem így történt.
persze ha a differenciálokkal írta volna fel.. és természetesen nem csak utalva a rel. Doppleres helyes alakra, hanem behelyettesítve.. akkor egy szavam sem lehetne.
DE mint olvasható mindhárom műben.. nem így történt.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16622):
1. rosszul emlekszel, ezt irtad:
mennyivel valtozik g erteke a nap felszinen a felszintol 1 meterre tavolodva?
Igazad van mikronrol mikronra valtozik a gravitacios allando, azonban a valtozas olyan kicsi, hogy allandonak tekintheto.
Probald meg, szamold ki az E=m*g*h keplettel a fold felszinen egy 1kg os targy helyzeti energiajat (1kg*9.81m/s2*1m), majd szamold ki ugyanezt ugy, hogy centimeterenkent kiszamolod a g ertekenek a valtozasat... vagy millimeterenkent... vagy integralsz.
2. szovegertesi negezsegeid vannak:
Az egzakt fizika azt mondja, hogy a keplet akkor igaz, HA a gravitacios allando erteke nem valtozik.
Hozzateszik, hogy egy peldaul egitest kozvetlen felszinen olyan kicsit valtozik, hogy allandonak tekintheto.
Amit te kritizalsz az a pelda, nem az egzakt fizika.
1. rosszul emlekszel, ezt irtad:
mennyivel valtozik g erteke a foldon a felszintol 1metert tavoldva?Mekkora ez az eltérés? Á, nem nagy 1 kg, és 1 m magasságnál csak E=1,5 mg*g*1 [J]
Persze 10 000 méteren és 100 000 kg esetében már sok-sok szorosa..
mennyivel valtozik g erteke a nap felszinen a felszintol 1 meterre tavolodva?
Igazad van mikronrol mikronra valtozik a gravitacios allando, azonban a valtozas olyan kicsi, hogy allandonak tekintheto.
Probald meg, szamold ki az E=m*g*h keplettel a fold felszinen egy 1kg os targy helyzeti energiajat (1kg*9.81m/s2*1m), majd szamold ki ugyanezt ugy, hogy centimeterenkent kiszamolod a g ertekenek a valtozasat... vagy millimeterenkent... vagy integralsz.
2. szovegertesi negezsegeid vannak:
Az egzakt fizika azt mondja, hogy a keplet akkor igaz, HA a gravitacios allando erteke nem valtozik.
Hozzateszik, hogy egy peldaul egitest kozvetlen felszinen olyan kicsit valtozik, hogy allandonak tekintheto.
Amit te kritizalsz az a pelda, nem az egzakt fizika.
0 x
A relativitási elméletek
@vaskalapos (16625): Még jó hogy kérdezted.. Mert 3,1e-6 m/s2 a helyes érték, és nem 1,5e-6, mint ahogy fentebb írtam.. (Bocs! A fél méteres szintkülönbség okozta eltérés számértékére emlékeztem az egy méteres helyett..)
A nap felszínén..g1m=7,87523E-07 m/s2
Bár jelzem, nem a nagyság, hanem az eltérés léte a lényeges.. Az olyan függvény amelyik statikus értékkel számol ilyen erősen változó értékek mellett az bizony eléggé gázos.
"Probald meg, szamold ki az E=m*g*h keplettel a fold felszinen egy 1kg os targy helyzeti energiajat (1kg*9.81m/s2*1m), majd szamold ki ugyanezt ugy, hogy centimeterenkent kiszamolod a g ertekenek a valtozasat... vagy millimeterenkent... vagy integralsz." Igen, megtettem. És?
Így ezzel a hibával 1 méter szintkülönbségnél már 1 ps eltérésnek kellene lennie.
A repülőgép magasságán (9600 m átlagot írtak) 90 ns a hiba.. Ami nagyobb mint az egyik irányban 24 óra alatti összes idő eltérés..:
A nap felszínén..g1m=7,87523E-07 m/s2
Bár jelzem, nem a nagyság, hanem az eltérés léte a lényeges.. Az olyan függvény amelyik statikus értékkel számol ilyen erősen változó értékek mellett az bizony eléggé gázos.
"Probald meg, szamold ki az E=m*g*h keplettel a fold felszinen egy 1kg os targy helyzeti energiajat (1kg*9.81m/s2*1m), majd szamold ki ugyanezt ugy, hogy centimeterenkent kiszamolod a g ertekenek a valtozasat... vagy millimeterenkent... vagy integralsz." Igen, megtettem. És?
Nos, nem. Mert ez a függvény igazából a gravitációs idődilatáció elvének alapja."2. szovegertesi negezsegeid vannak:
Az egzakt fizika azt mondja, hogy a keplet akkor igaz, HA a gravitacios allando erteke nem valtozik.
Hozzateszik, hogy egy peldaul egitest kozvetlen felszinen olyan kicsit valtozik, hogy allandonak tekintheto.
"
Így ezzel a hibával 1 méter szintkülönbségnél már 1 ps eltérésnek kellene lennie.
A repülőgép magasságán (9600 m átlagot írtak) 90 ns a hiba.. Ami nagyobb mint az egyik irányban 24 óra alatti összes idő eltérés..:
eastward 144±14 −184 ± 18 −40 ± 23 −59 ± 10
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16627):
Mennyi a kulonbseg?
2. akkor nem is az olvasott konyveket kritizalod, hanem egy regi kiserletet. megegyezuk, hogy a konyvek rendben vannak.
Allando gravitacios terre vezettek le az elmeletet.
Arra szerinted is igaz, ugye?
"Probald meg, szamold ki az E=m*g*h keplettel a fold felszinen egy 1kg os targy helyzeti energiajat (1kg*9.81m/s2*1m), majd szamold ki ugyanezt ugy, hogy centimeterenkent kiszamolod a g ertekenek a valtozasat... vagy millimeterenkent... vagy integralsz." Igen, megtettem. És?
Mennyi a kulonbseg?
1. Ezt le tudnad vezetni leperol lepesre?Így ezzel a hibával 1 méter szintkülönbségnél már 1 ps eltérésnek kellene lennie.
2. akkor nem is az olvasott konyveket kritizalod, hanem egy regi kiserletet. megegyezuk, hogy a konyvek rendben vannak.
Allando gravitacios terre vezettek le az elmeletet.
Arra szerinted is igaz, ugye?
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16627):
Nekem gyanus, hogy csak kb tizszeres elteres val a foldon es napon az 1meter magassag okozta gravitacio valtozas kozott, mikorben a sugarak ennel tobb nagysagranddel jobban elternek.
Lehet, hogy igazad van, de erdeklodva kovetnem hogyan szamoltal?
erre gondolsz?Még jó hogy kérdezted.. Mert 3,1e-6 m/s2 a helyes érték, és nem 1,5e-6, mint ahogy fentebb írtam.. (Bocs! A fél méteres szintkülönbség okozta eltérés számértékére emlékeztem az egy méteres helyett..)
Nalam a 10-6 is hianyzik, az az igazi gaz...Mekkora ez az eltérés? Á, nem nagy 1 kg, és 1 m magasságnál csak E=1,5 mg*g*1 [J]
Ezt hogyan szamoltad ki?A nap felszínén..g1m=7,87523E-07 m/s2
Nekem gyanus, hogy csak kb tizszeres elteres val a foldon es napon az 1meter magassag okozta gravitacio valtozas kozott, mikorben a sugarak ennel tobb nagysagranddel jobban elternek.
Lehet, hogy igazad van, de erdeklodva kovetnem hogyan szamoltal?
0 x
A relativitási elméletek
@vaskalapos (16633): Na figyelj! Ennyire ne legyél amatör!: Nalam a 10-6 is hianyzik, az az igazi gaz...
1 kg= 1000 g = 1000 000 mg a mértékegységben van amit kerestél..
g2=6,67428E-11*1,9891E+30/ (6,96E8+1)2=274,0580474 m/s2
g1-g2= 7,87523E-7 m/s2
"Nekem gyanus, hogy csak kb tizszeres elteres val a foldon es napon az 1meter magassag okozta gravitacio valtozas kozott, mikorben a sugarak ennel tobb nagysagranddel jobban elternek."
Nos, ha csak gyanús, arra egy exceles szorzás megoldás lehet, mert az csodákra képes
Allando gravitacios terre vezettek le az elmeletet.
Arra szerinted is igaz, ugye?
Nos éppen ez a baj.. Mert így csak az állandó grav. térre lehetne érvényes, a valós (földi, napi, stb.) égitestek esetében nem..
Csodás módon mégis azt valljuk, hogy a GPS holdak esetében, "működik"
pedig 350 km magasan a valós eltérésnek már dg=0,99869 m/s2 már nagyon nagy 10%!!! hibát kellene okoznia.
1 kg= 1000 g = 1000 000 mg a mértékegységben van amit kerestél..
g1=6,67428E-11*1,9891E+30/ (6,96E8)2=274,0580482 m/s2A nap felszínén..g1m=7,87523E-07 m/s2
Ezt hogyan szamoltad ki?
g2=6,67428E-11*1,9891E+30/ (6,96E8+1)2=274,0580474 m/s2
g1-g2= 7,87523E-7 m/s2
"Nekem gyanus, hogy csak kb tizszeres elteres val a foldon es napon az 1meter magassag okozta gravitacio valtozas kozott, mikorben a sugarak ennel tobb nagysagranddel jobban elternek."
Nos, ha csak gyanús, arra egy exceles szorzás megoldás lehet, mert az csodákra képes
Allando gravitacios terre vezettek le az elmeletet.
Arra szerinted is igaz, ugye?
Nos éppen ez a baj.. Mert így csak az állandó grav. térre lehetne érvényes, a valós (földi, napi, stb.) égitestek esetében nem..
Csodás módon mégis azt valljuk, hogy a GPS holdak esetében, "működik"
pedig 350 km magasan a valós eltérésnek már dg=0,99869 m/s2 már nagyon nagy 10%!!! hibát kellene okoznia.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16637):
Fel sem merult bennem, hogy egy kepletbe beirsz egy mertekegyseget.
mivel m*g-rol szol a keplet a mg-t sajtohibanak gondoltam.
E=1,5 mg*g*1 [J]
bizarr
a [J] az mi? vagy J abszolut erteke?
vagy az E mertekegyseg, joule?
Fel sem merult bennem, hogy egy kepletbe beirsz egy mertekegyseget.
mivel m*g-rol szol a keplet a mg-t sajtohibanak gondoltam.
E=1,5 mg*g*1 [J]
bizarr
a [J] az mi? vagy J abszolut erteke?
vagy az E mertekegyseg, joule?
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16637):
Es ugyanez a Fold felszinen? [nem akarok mas adatokkal szamolni, mint amikkel te szamoltal. Fold sugara, Fold tomege amikkel te szamoltal?
A fenti szamolasnal melyik szam mit jelent?g1=6,67428E-11*1,9891E+30/ (6,96E8)2=274,0580482 m/s2
g2=6,67428E-11*1,9891E+30/ (6,96E8+1)2=274,0580474 m/s2
g1-g2= 7,87523E-7 m/s2
"Nekem gyanus, hogy csak kb tizszeres elteres val a foldon es napon az 1meter magassag okozta gravitacio valtozas kozott, mikorben a sugarak ennel tobb nagysagranddel jobban elternek."
Nos, ha csak gyanús, arra egy exceles szorzás megoldás lehet, mert az csodákra képes
Es ugyanez a Fold felszinen? [nem akarok mas adatokkal szamolni, mint amikkel te szamoltal. Fold sugara, Fold tomege amikkel te szamoltal?
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16637):
Korabban a kiserletet kritizaltad tobb hozzaszolason keresztul.
Nem vilagos, hogy a GPS-nel miert valtozna a g erteke?
350km-t valtozik a muhold magassaga keringese soran?
Nem elegendo ott azzal a g-vel szamolni ami ott merheto?
Nem vilagos, hogy az elmeletet kritizalod, vagy kiserletet?Allando gravitacios terre vezettek le az elmeletet.
Arra szerinted is igaz, ugye?Nos éppen ez a baj.. Mert így csak az állandó grav. térre lehetne érvényes, a valós (földi, napi, stb.) égitestek esetében nem..
Csodás módon mégis azt valljuk, hogy a GPS holdak esetében, "működik"
pedig 350 km magasan a valós eltérésnek már dg=0,99869 m/s2 már nagyon nagy 10%!!! hibát kellene okoznia.
Korabban a kiserletet kritizaltad tobb hozzaszolason keresztul.
Nem vilagos, hogy a GPS-nel miert valtozna a g erteke?
350km-t valtozik a muhold magassaga keringese soran?
Nem elegendo ott azzal a g-vel szamolni ami ott merheto?
0 x
A relativitási elméletek
@vaskalapos (16651):
g1=k*M/R2=6,67428E-11* 5,9742E24/ 63727972=9,8383877247114 m/s2
g2=k*M/R2=6,67428E-11* 5,9742E24/ (6372797+1)2=9,8383846338914 m/s2
g1-g2=3,090819931E-06 m/s2
Nem vilagos, hogy az elmeletet kritizalod, vagy kiserletet?
Korabban a kiserletet kritizaltad tobb hozzaszolason keresztul.
Igazából mindkettőt.. A felszínhez relatív mozgás kelet-nyugat irányban is a felszínhez relatív.. Csak a naphoz vagy a galaxishoz relatívan lehet eltérő..
A másik, hogy maga az elv is sántít. Nem állandó a gravitációs térerősség. Ezáltal ha helyesen is mértek volna a repülőkön, az átlag magassággal önmagában bukott volna a kísérleti igazolás.
Ami pedig az elméletet illeti.. azt már leírtam.. kimaradt a lényeg, a rel.Doppleres függvény a magasságfüggő térerősséggel. Innentől az egész úgy rossz ahogy van.
Mert ha egy téridő geometriában az időfüggvény rossz, akkor minden pontján rossz a képzett idő.
g1=k*M/R2=6,67428E-11* 5,9742E24/ 63727972=9,8383877247114 m/s2
g2=k*M/R2=6,67428E-11* 5,9742E24/ (6372797+1)2=9,8383846338914 m/s2
g1-g2=3,090819931E-06 m/s2
Nem vilagos, hogy az elmeletet kritizalod, vagy kiserletet?
Korabban a kiserletet kritizaltad tobb hozzaszolason keresztul.
Igazából mindkettőt.. A felszínhez relatív mozgás kelet-nyugat irányban is a felszínhez relatív.. Csak a naphoz vagy a galaxishoz relatívan lehet eltérő..
A másik, hogy maga az elv is sántít. Nem állandó a gravitációs térerősség. Ezáltal ha helyesen is mértek volna a repülőkön, az átlag magassággal önmagában bukott volna a kísérleti igazolás.
Ami pedig az elméletet illeti.. azt már leírtam.. kimaradt a lényeg, a rel.Doppleres függvény a magasságfüggő térerősséggel. Innentől az egész úgy rossz ahogy van.
Mert ha egy téridő geometriában az időfüggvény rossz, akkor minden pontján rossz a képzett idő.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@vaskalapos (16660):  Hát ez az..
Hát ez az..
Ez is egy olyan eset, amikor a természet szerencsére nagy ívben tesz a modellekben leírtakra..
Ez is egy olyan eset, amikor a természet szerencsére nagy ívben tesz a modellekben leírtakra..
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16654):
Koszi.
Tehat a fold felszinen 1 meter magassagkulonbseg 3*10-5 % valtozast eredmenyez a gravitacios allandoban, a nap felszinen az 1 meter 3*10-14 % kulonbseget okoz.
a 3*10-14 % kulonbseg....
Koszi.
Tehat a fold felszinen 1 meter magassagkulonbseg 3*10-5 % valtozast eredmenyez a gravitacios allandoban, a nap felszinen az 1 meter 3*10-14 % kulonbseget okoz.
a 3*10-14 % kulonbseg....
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16661):
Valami kulonos oknal fogva a modell alapjan irt program szamomra elegseges pontossagggal mutatja a kocsim helyzetet az uton.
A termeszet csinal amit akar, szamomra elfogadhato az a modell, ami alapjan tudok navigalni.
A GPS-t emberek terveztek es emberek programoztak a modellek alapjan.Ez is egy olyan eset, amikor a természet szerencsére nagy ívben tesz a modellekben leírtakra..
Valami kulonos oknal fogva a modell alapjan irt program szamomra elegseges pontossagggal mutatja a kocsim helyzetet az uton.
A termeszet csinal amit akar, szamomra elfogadhato az a modell, ami alapjan tudok navigalni.
0 x
A relativitási elméletek
@vaskalapos (16668): Csak jelzem:
ez kicsit több mint "3*10-14 % kulonbseget okoz.""g1=6,67428E-11*1,9891E+30/ (6,96E8)2=274,0580482 m/s2
g2=6,67428E-11*1,9891E+30/ (6,96E8+1)2=274,0580474 m/s2
g1-g2= 7,87523E-7 m/s2
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (16674):
Igazad van, atmasoltam a szamaidat Excelbe, es a tizedesvesszoodet egy helyen elfelejtettem tizedespontra cserelni.
Az en hibam. A helyes ertek 3*10-7% a nap eseten.
OFF
a magyar nyelvu excel tizedesvesszokkel dolgozik, vagy tizedesponttal?
/OFF
Igazad van, atmasoltam a szamaidat Excelbe, es a tizedesvesszoodet egy helyen elfelejtettem tizedespontra cserelni.
Az en hibam. A helyes ertek 3*10-7% a nap eseten.
OFF
a magyar nyelvu excel tizedesvesszokkel dolgozik, vagy tizedesponttal?
/OFF
0 x
A relativitási elméletek
@vaskalapos (16678): Így érthető.. egyszerű elírás..
Az enyém tizedes vesszővel.
Az enyém tizedes vesszővel.
0 x
A relativitási elméletek
Emeljük kicsit a színvonalat:
Akik azt mondják, hogy a relativisztikus effektusok nem valódiak (látszólagosak), azok miért gondolják így és mit értenek alatta?
Akik azt mondják, hogy a relativisztikus effektusok nem valódiak (látszólagosak), azok miért gondolják így és mit értenek alatta?
0 x
A relativitási elméletek
@ge3lan (17285):
Első feleként a valódiságáról érdemes szólni. Legyen egy IR-ben nyugvó merev test két pontja közötti koordináták x távolsága.
Ha nem hat ható, akkor nincs ok ami okozatot válthatna ki. Ez alapismeret. Azaz ez a "valódi" x távolság állandó. Hiába nézi és látja ezernyi, milliónyi, különféle sebességgel mozgó megfigyelő különféle hosszúságúnak, a valódi hossza ok hiányában változatlan.
Akkor miért nem ilyennek látjuk ha mozog hozzánk viszonyítva?
Erre a másodikként a jeltovábbítás sajátosságát mint ok-okozat alapját találjuk.
Ha végtelenül nagy sebességgel, azaz azonnal megérkezne az x távolság végpontjainak a koordinátáiról a jel mindenkihez, akkor mindenki ugyanazt az x távolságot mérhetné.
Csakhogy a hang, a teknősbéka, vagy akár a fény véges sebességgel mozog.
Ebből következően a megfigyelt mozgásának v sebességének és a jeltovábbítás c sebességének:
ß=c/gyök(c2-v2)=1/sin(arccos(v/c))=1/gyök(1-v2/c2) arányában érkezik a megfigyelőhöz a megfigyelt x távolság végpontjairól a koordinátákról tudósító jel.
Azaz az okozat az x távolság helyett x' távolság mérésének lehetősége, amelynek egyszerű oka a jeltovábbítás sebességének és a mozgási sebességnek az aránya.
Arra a kérdésre, hogy ez látszat-e vagy lehetne-e valóság nagyon egyszerűen felelhetünk. A fény helyett használjunk egy szintén állandó sebességű jelet.
A jel állandó sebessége Einstein szerint minden megfigyelőhöz viszonyítva "egyszerre" állandó.
Azaz ezzel a forrásához állandóság is szerepel a "minden megfigyelőhöz viszonyítva "egyszerre" állandó " felsorolásban.
Így a kérdés eldöntéséhez szükséges és elégséges feltételként megállapítható, hogy ha ugyanazon függvény szerint arányul a más jeltovábbítási sebesség sebesség mellett is x és x' távolság, mint a fény sebessége mint jeltovábbító sebesség mellett,
akkor az azonos ok-okozat összefüggés van az x' érték képzésekor mint a fény esetében.
Azaz képezzünk a fényóra mintájára, azonos elrendezéssel hang órát!
Amelynek visszaverő felületei között "pattogjon a hang" c hangsebességgel, és mozogjunk a hang órához viszonyítva v sebességgel.. azaz a hang óra mozogjon a koordináta rendszerünkben v sebességgel.
A mi koordináta rendszerünk minden pontján álljon egy megfigyelőnk a rendszerben szinkronozott órával.
Így a hang óra végpontjain megjelenő hang helyét és időpontját regisztrálhatjuk a mi koordináta rendszerünkben.
Itt jegyzendő meg, hogy a fény fotonjának haladás közbeni helyét nem ismerjük, csak azon pontjait az útvonalának, ahol a tükrökkel találkozik.
Ezért elegendő az is, ha a hanghullám haladás közbeni helye helyett szintén csak a végpontok azaz a tükrök helyénél megjelenését regisztráljuk, ugyanúgy mint fény esetében.
Ekkor a hanggal: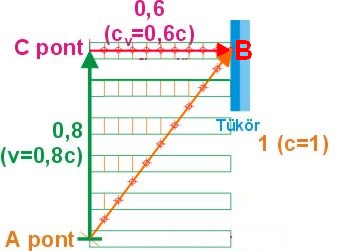 a kapott függvény:
a kapott függvény:
ß=c/gyök(c2-v2)=1/sin(arccos(v/c))=1/gyök(1-v2/c2)
Az azonos alakú függvényből következően, azonos x' távolság adódik az x távolságból. Nyilván a kontrahálódott x' távolsággal és a c jeltovábbítási sebességgel éppen úgy t' dilatáció idő számítható mint fény esetében.
Azaz a c és v sebességek adta ß arányban minden Lorentz transzformáció egyaránt azonos eredményeket ad, a fény esetében mért értékekkel.
Vagyis, ha az óra mutatók állását a hang mint jel közvetíti a mozgó rendszerek között, akkor például a relatív egyidejűség függvénye szintén helyes tau idő különbözetet ad a mozgó rendszerben egyidejű események megfigyelése esetén az események időpontjai közötti eltérésre.
Így felvethető a látszólagosság kérdése: Ha a tényleges v sebesség nagyságától függetlenül, kizárólag a jeltovábbítás c sebességének a relatív mozgás v sebességéhez viszonyított
ß=c/gyök(c2-v2)=1/sin(arccos(v/c))=1/gyök(1-v2/c2) arányától függenek a mérések adta eredmények, akkor mennyire "látszólagosak" a méréssel kapott eredmények?
A logika szabálya szerint ha a relatív sebesség nagyságától független a transzformációkkal kapott távolság,- időn- stb. arány, mert kizárólag a relatív mozgás sebességének a jeltovábbítás sebességéhez viszonyításából származó ez az arány,
akkor csupán látszat, tulajdonképpen szimpla mérési hiba.
Azaz ez a látszat egy olyan mérési hiba, amely minden olyan típusú mérésnél megjelenik, ahol a mérést végző és a mérendő között v sebességű relatív mozgás társul c sebességű jeltovábbítási sebességhez.
Így a logika szerint ezt a hibát kompenzálni kell a valós mérési eredmények képzéséhez.
A kompenzálás módszere adott: Lorentz transzformáció.
Tehát ha a Lorentz transzformációk segítségével a méréssel kapott adatokat a saját rendszerünkben érvényes, hiba mentes valósággá transzformáljuk, akkor megkapjuk a látszat szerinti eredményekből a történések valóságos adatait.
Azaz ha a látszat szerint x' a távolság egy merev test két végpontja között, akkor
a transzformálással megkapott x távolságról tudjuk, hogy ez az x távolság már nem tartalmazza a jeltovábbítás sebességéből adódó hibát, hiszen a transzformációval a hiba kompenzálást elvégeztük, így mindkét rendszerben a merev test végpontjai közötti valós távolság x.
Persze ha tudatlanságból, misztifikálni akarunk, akkor jöhetünk olyan ok-okozati összefüggést nélkülöző mende-mondákkal, hogy valóságos a méréssel kapott x' távolság.
Egyébként pedig a "tét emelése" előtti mondatokat felidézve, a relativitás generális teóriája nem csak a távolság függő g nagysága miatt érdekes, hanem a tömeg távolság függő nagysága miatt is.
Hiszen azt is tudjuk, hogy ha E energiát elnyel egy adott m0 tömeg, akkor
m=m0+E/c2 tömeggé alakul.
Azaz az R távolság függvényében az erő nagyságát nem csak a változó nagyságú g hanem a szintén változó nagyságú m tömeg is meghatározza.
Így ha Lebegyev kijavított levezetését alkalmazzuk a gravitációra, vagyis:
p*v=m*c2 azaz F*v/A=m*c2 ahol A=m/(d*ρ) [ az m tömeg vm térfogatából, amelyben vm=A*d és az anyag sűrűsége ρ=m/v] , valamint F=m*k*M/R2
akkor miután mindkét test a másik test által kisugárzott energia hatására gyorsul, a köztük lévő l távolság megváltozása nem csak az egyik test elmozdulásának eredménye, mint ahogyan Einstein számolt vele, még jobban látszik, hogy mennyire pontatlan és hiányos a teória geometriai analógiára épített elve.
Hogy szemléletesebben látható legyen, vegyük az m=M esetet, amelyben mindkét tömeg egyidejű elmozdulása révén az E=m*g*h függvény helyett, a csak matematikailag azonos
alakra hozható E+E=m*g*h/2+M*g*h/2 okán,
Δg= k*m/R2 - k*m/(R+h/2)2
Vagyis a g négy változós függvény szerint, az energia és az m valamint M tömeg a gm és gM függvényében változik, és ez a sugárzással terjedő hatás még a relatív sebesség függvényében a rel.Doppler szerint úgy módosul, hogy a v relatív sebességet a lokális g okozta idő lassulás mértékében más értékűnek méri minden megfigyelő.
Ha még a helyi g különbözetek függvényében fellépő erők hatására létrejövő alaki illetve ezzel sűrűségi deformáció-torzulás hosszmérce változtató hatását is figyelembe vesszük,
akkor is marad olyan tényező amit még ezek után sem vettünk számításba.
Szumma szummárum, Einstein elméletének sem az elve, sem a pontossága nem hibátlan.
A pontosságán az elvi hibája révén nem lehet javítani. Így mint ahogy a specrel két mérési hiba létére alapozottsága mutatta, hogy érdemes új elvekkel helyettesíteni, úgy a hibás specrelre alapozott, majd újabb elvi hibákkal teletűzdelt áltrelt is helyettesíteni kellene egy sokkal helyesebb elvi megközelítést alkalmazó elmélettel.
A kérdés felvetés egyben többszörös.Akik azt mondják, hogy a relativisztikus effektusok nem valódiak (látszólagosak), azok miért gondolják így és mit értenek alatta?
Első feleként a valódiságáról érdemes szólni. Legyen egy IR-ben nyugvó merev test két pontja közötti koordináták x távolsága.
Ha nem hat ható, akkor nincs ok ami okozatot válthatna ki. Ez alapismeret. Azaz ez a "valódi" x távolság állandó. Hiába nézi és látja ezernyi, milliónyi, különféle sebességgel mozgó megfigyelő különféle hosszúságúnak, a valódi hossza ok hiányában változatlan.
Akkor miért nem ilyennek látjuk ha mozog hozzánk viszonyítva?
Erre a másodikként a jeltovábbítás sajátosságát mint ok-okozat alapját találjuk.
Ha végtelenül nagy sebességgel, azaz azonnal megérkezne az x távolság végpontjainak a koordinátáiról a jel mindenkihez, akkor mindenki ugyanazt az x távolságot mérhetné.
Csakhogy a hang, a teknősbéka, vagy akár a fény véges sebességgel mozog.
Ebből következően a megfigyelt mozgásának v sebességének és a jeltovábbítás c sebességének:
ß=c/gyök(c2-v2)=1/sin(arccos(v/c))=1/gyök(1-v2/c2) arányában érkezik a megfigyelőhöz a megfigyelt x távolság végpontjairól a koordinátákról tudósító jel.
Azaz az okozat az x távolság helyett x' távolság mérésének lehetősége, amelynek egyszerű oka a jeltovábbítás sebességének és a mozgási sebességnek az aránya.
Arra a kérdésre, hogy ez látszat-e vagy lehetne-e valóság nagyon egyszerűen felelhetünk. A fény helyett használjunk egy szintén állandó sebességű jelet.
A jel állandó sebessége Einstein szerint minden megfigyelőhöz viszonyítva "egyszerre" állandó.
Azaz ezzel a forrásához állandóság is szerepel a "minden megfigyelőhöz viszonyítva "egyszerre" állandó " felsorolásban.
Így a kérdés eldöntéséhez szükséges és elégséges feltételként megállapítható, hogy ha ugyanazon függvény szerint arányul a más jeltovábbítási sebesség sebesség mellett is x és x' távolság, mint a fény sebessége mint jeltovábbító sebesség mellett,
akkor az azonos ok-okozat összefüggés van az x' érték képzésekor mint a fény esetében.
Azaz képezzünk a fényóra mintájára, azonos elrendezéssel hang órát!
Amelynek visszaverő felületei között "pattogjon a hang" c hangsebességgel, és mozogjunk a hang órához viszonyítva v sebességgel.. azaz a hang óra mozogjon a koordináta rendszerünkben v sebességgel.
A mi koordináta rendszerünk minden pontján álljon egy megfigyelőnk a rendszerben szinkronozott órával.
Így a hang óra végpontjain megjelenő hang helyét és időpontját regisztrálhatjuk a mi koordináta rendszerünkben.
Itt jegyzendő meg, hogy a fény fotonjának haladás közbeni helyét nem ismerjük, csak azon pontjait az útvonalának, ahol a tükrökkel találkozik.
Ezért elegendő az is, ha a hanghullám haladás közbeni helye helyett szintén csak a végpontok azaz a tükrök helyénél megjelenését regisztráljuk, ugyanúgy mint fény esetében.
Ekkor a hanggal:
 a kapott függvény:
a kapott függvény:ß=c/gyök(c2-v2)=1/sin(arccos(v/c))=1/gyök(1-v2/c2)
Az azonos alakú függvényből következően, azonos x' távolság adódik az x távolságból. Nyilván a kontrahálódott x' távolsággal és a c jeltovábbítási sebességgel éppen úgy t' dilatáció idő számítható mint fény esetében.
Azaz a c és v sebességek adta ß arányban minden Lorentz transzformáció egyaránt azonos eredményeket ad, a fény esetében mért értékekkel.
Vagyis, ha az óra mutatók állását a hang mint jel közvetíti a mozgó rendszerek között, akkor például a relatív egyidejűség függvénye szintén helyes tau idő különbözetet ad a mozgó rendszerben egyidejű események megfigyelése esetén az események időpontjai közötti eltérésre.
Így felvethető a látszólagosság kérdése: Ha a tényleges v sebesség nagyságától függetlenül, kizárólag a jeltovábbítás c sebességének a relatív mozgás v sebességéhez viszonyított
ß=c/gyök(c2-v2)=1/sin(arccos(v/c))=1/gyök(1-v2/c2) arányától függenek a mérések adta eredmények, akkor mennyire "látszólagosak" a méréssel kapott eredmények?
A logika szabálya szerint ha a relatív sebesség nagyságától független a transzformációkkal kapott távolság,- időn- stb. arány, mert kizárólag a relatív mozgás sebességének a jeltovábbítás sebességéhez viszonyításából származó ez az arány,
akkor csupán látszat, tulajdonképpen szimpla mérési hiba.
Azaz ez a látszat egy olyan mérési hiba, amely minden olyan típusú mérésnél megjelenik, ahol a mérést végző és a mérendő között v sebességű relatív mozgás társul c sebességű jeltovábbítási sebességhez.
Így a logika szerint ezt a hibát kompenzálni kell a valós mérési eredmények képzéséhez.
A kompenzálás módszere adott: Lorentz transzformáció.
Tehát ha a Lorentz transzformációk segítségével a méréssel kapott adatokat a saját rendszerünkben érvényes, hiba mentes valósággá transzformáljuk, akkor megkapjuk a látszat szerinti eredményekből a történések valóságos adatait.
Azaz ha a látszat szerint x' a távolság egy merev test két végpontja között, akkor
a transzformálással megkapott x távolságról tudjuk, hogy ez az x távolság már nem tartalmazza a jeltovábbítás sebességéből adódó hibát, hiszen a transzformációval a hiba kompenzálást elvégeztük, így mindkét rendszerben a merev test végpontjai közötti valós távolság x.
Persze ha tudatlanságból, misztifikálni akarunk, akkor jöhetünk olyan ok-okozati összefüggést nélkülöző mende-mondákkal, hogy valóságos a méréssel kapott x' távolság.
Egyébként pedig a "tét emelése" előtti mondatokat felidézve, a relativitás generális teóriája nem csak a távolság függő g nagysága miatt érdekes, hanem a tömeg távolság függő nagysága miatt is.
Hiszen azt is tudjuk, hogy ha E energiát elnyel egy adott m0 tömeg, akkor
m=m0+E/c2 tömeggé alakul.
Azaz az R távolság függvényében az erő nagyságát nem csak a változó nagyságú g hanem a szintén változó nagyságú m tömeg is meghatározza.
Így ha Lebegyev kijavított levezetését alkalmazzuk a gravitációra, vagyis:
p*v=m*c2 azaz F*v/A=m*c2 ahol A=m/(d*ρ) [ az m tömeg vm térfogatából, amelyben vm=A*d és az anyag sűrűsége ρ=m/v] , valamint F=m*k*M/R2
akkor miután mindkét test a másik test által kisugárzott energia hatására gyorsul, a köztük lévő l távolság megváltozása nem csak az egyik test elmozdulásának eredménye, mint ahogyan Einstein számolt vele, még jobban látszik, hogy mennyire pontatlan és hiányos a teória geometriai analógiára épített elve.
Hogy szemléletesebben látható legyen, vegyük az m=M esetet, amelyben mindkét tömeg egyidejű elmozdulása révén az E=m*g*h függvény helyett, a csak matematikailag azonos
alakra hozható E+E=m*g*h/2+M*g*h/2 okán,
Δg= k*m/R2 - k*m/(R+h/2)2
Vagyis a g négy változós függvény szerint, az energia és az m valamint M tömeg a gm és gM függvényében változik, és ez a sugárzással terjedő hatás még a relatív sebesség függvényében a rel.Doppler szerint úgy módosul, hogy a v relatív sebességet a lokális g okozta idő lassulás mértékében más értékűnek méri minden megfigyelő.
Ha még a helyi g különbözetek függvényében fellépő erők hatására létrejövő alaki illetve ezzel sűrűségi deformáció-torzulás hosszmérce változtató hatását is figyelembe vesszük,
akkor is marad olyan tényező amit még ezek után sem vettünk számításba.
Szumma szummárum, Einstein elméletének sem az elve, sem a pontossága nem hibátlan.
A pontosságán az elvi hibája révén nem lehet javítani. Így mint ahogy a specrel két mérési hiba létére alapozottsága mutatta, hogy érdemes új elvekkel helyettesíteni, úgy a hibás specrelre alapozott, majd újabb elvi hibákkal teletűzdelt áltrelt is helyettesíteni kellene egy sokkal helyesebb elvi megközelítést alkalmazó elmélettel.
0 x
A relativitási elméletek
@Gábor (17835): Az einsteini képlet hibája = 100 - a nagy precizitású mérési eredmény 0,037"/ einsteini képlettel 0,041" *100=9,7561 %
Azaz Einstein függvényének hibája a 17 hónapos és 750 000 000 $ árú szuper precíz mérés eredményeként 9,7561 %
Tehát minél pontosabban akarjuk igazolni Einstein elveit annál pontatlanabbnak bizonyulnak ezen elvek.
Ennek okai a rossz alapfelvetésekből adódó beépített hibák léte.
Lásd fentebbi levezetéseket, kiemeléseket!
"Einstein képletei azt is megmondják, mennyivel: évenként 0,041 szögmásodperccel. A mérések 0,037 szögmásodpercet mutattak, ami azt jelenti, hogy a jelenség létezését sikerült igazolni, de vagy a műszer, vagy a mérési módszer, vagy a képlet nem teljesen pontos.
A giroszkópos ötletet 1959-ben vetették fel a NASA fizikusai, és az űrhivatal hivatalosan 1963-ban indította el a kísérletet. A technikai korlátok évtizedekig leküzdhetetlennek tűntek, összesen hétszer állították le, majd indították újra a projektek, hogy végül 2004-ben Föld körüli pályára bocsássák a 750 millió dollárból megépített szondát.
A Gravity Probe B 17 hónapon át gyűjtötte az adatokat, amelyeknek a kielemzése mostanáig tartott. A tudósok szerint mindenképpen a fizika történetének klasszikus kísérletei között van a helye a NASA fél évszázados küzdelmének Einstein teóriájának bebizonyításával."
Már a Schwarzschild téridő sem tesz lehetővé pontos számításokat a g-vel változó nagyságú tömeg következtében. Einstein függvényeiben még a g statikus értékével is további hibákat épített be.
Így ahelyett, hogy igazolná, mint írja a cikk, egyenes cáfolata Einstein teóriájának minden precízen elvégzett mérés eredménye.
Azaz Einstein függvényének hibája a 17 hónapos és 750 000 000 $ árú szuper precíz mérés eredményeként 9,7561 %
Tehát minél pontosabban akarjuk igazolni Einstein elveit annál pontatlanabbnak bizonyulnak ezen elvek.
Ennek okai a rossz alapfelvetésekből adódó beépített hibák léte.
Lásd fentebbi levezetéseket, kiemeléseket!
"Einstein képletei azt is megmondják, mennyivel: évenként 0,041 szögmásodperccel. A mérések 0,037 szögmásodpercet mutattak, ami azt jelenti, hogy a jelenség létezését sikerült igazolni, de vagy a műszer, vagy a mérési módszer, vagy a képlet nem teljesen pontos.
A giroszkópos ötletet 1959-ben vetették fel a NASA fizikusai, és az űrhivatal hivatalosan 1963-ban indította el a kísérletet. A technikai korlátok évtizedekig leküzdhetetlennek tűntek, összesen hétszer állították le, majd indították újra a projektek, hogy végül 2004-ben Föld körüli pályára bocsássák a 750 millió dollárból megépített szondát.
A Gravity Probe B 17 hónapon át gyűjtötte az adatokat, amelyeknek a kielemzése mostanáig tartott. A tudósok szerint mindenképpen a fizika történetének klasszikus kísérletei között van a helye a NASA fél évszázados küzdelmének Einstein teóriájának bebizonyításával."
Már a Schwarzschild téridő sem tesz lehetővé pontos számításokat a g-vel változó nagyságú tömeg következtében. Einstein függvényeiben még a g statikus értékével is további hibákat épített be.
Így ahelyett, hogy igazolná, mint írja a cikk, egyenes cáfolata Einstein teóriájának minden precízen elvégzett mérés eredménye.
0 x
A relativitási elméletek
@Gézoo (17852):
A szonda egyebkent ket dolgot mert:
"geodetic effect: -6,602 mas/yr (milli-arcseconds per year)
GR: -6,606 mas/yr "
Az elteres 0.06%, a meres hibaja 0.3%
A nehezebb meres a "frame-dragging"
-37.2 mas/yr
GR: -39.2 mas/yr
elteres: 7%, meres hibaja: 19%
Az ilyesfele eredmenyeket egyezesnek hivjak.
A meres hibaja 20%-volt, ugyhogy ezt a merest a "stimmel" rublikaba irhatjuk.Azaz Einstein függvényének hibája a 17 hónapos és 750 000 000 $ árú szuper precíz mérés eredményeként 9,7561 %
Igen, kiveve az osszes merest amit eddig vegeztek. De elobb-utobb biztos lesz egy ami megmutatja az elmelet hatarait.egyenes cáfolata Einstein teóriájának minden precízen elvégzett mérés eredménye.
A szonda egyebkent ket dolgot mert:
"geodetic effect: -6,602 mas/yr (milli-arcseconds per year)
GR: -6,606 mas/yr "
Az elteres 0.06%, a meres hibaja 0.3%
A nehezebb meres a "frame-dragging"
-37.2 mas/yr
GR: -39.2 mas/yr
elteres: 7%, meres hibaja: 19%
Az ilyesfele eredmenyeket egyezesnek hivjak.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (17852):
Bemutatnad itt, hogy a te konkretan milyen erteket szamolsz ugyanerre problemara az altalad helyesnek tartott elmelet alapjan?Ennek okai a rossz alapfelvetésekből adódó beépített hibák léte.
Lásd fentebbi levezetéseket, kiemeléseket!
"Einstein képletei azt is megmondják, mennyivel: évenként 0,041 szögmásodperccel. A mérések 0,037 szögmásodpercet mutattak,
0 x
A relativitási elméletek
@vaskalapos (17857): Konkrétan nem tudok olyan elméletről amely helyesen számolna.
Én csak elemeztem Einstein teóriáit, és levezettem azt, hogy a hibás részek miért hibásak.
Az áltrel is, hasonlóan a specrelhez, használhatóvá tehető lenne, ha a helyes összefüggésekre cserélnénk Einstein hibás függvényeit.
Itt van például az alap, a gravitációs potenciál helyes értéke. Egyenlőre még nem íródott olyan levezetés amely 3-5 tizedes pontossággal megfelelne a fizikai mérésekben kapott értékeknek.
Nem árulok el túl nagy titkot ha azt írom, hogy már gondoltam arra, hogy ha az a sok híres fizikus nem tudta levezetni, akkor talán neki kellene állnia olyannak aki képes rá.
Na de van olyan, az elődeinél sokkal nagyobb tudású élő fizikus?
Én csak elemeztem Einstein teóriáit, és levezettem azt, hogy a hibás részek miért hibásak.
Az áltrel is, hasonlóan a specrelhez, használhatóvá tehető lenne, ha a helyes összefüggésekre cserélnénk Einstein hibás függvényeit.
Itt van például az alap, a gravitációs potenciál helyes értéke. Egyenlőre még nem íródott olyan levezetés amely 3-5 tizedes pontossággal megfelelne a fizikai mérésekben kapott értékeknek.
Nem árulok el túl nagy titkot ha azt írom, hogy már gondoltam arra, hogy ha az a sok híres fizikus nem tudta levezetni, akkor talán neki kellene állnia olyannak aki képes rá.
Na de van olyan, az elődeinél sokkal nagyobb tudású élő fizikus?
0 x
A relativitási elméletek
@Gézoo (17287):
nagyon érdekel a téma, ezért regiztem, csak egy dolgot nem értek:
ebből a válaszodból még mindig nem látszik mi a különbség a valódi és a nem valódi hossz között. vagy ´te azt a hosszt érted valódinak, amit akkor mérünk, ha nyugalomban van?
nagyon érdekel a téma, ezért regiztem, csak egy dolgot nem értek:
ebből a válaszodból még mindig nem látszik mi a különbség a valódi és a nem valódi hossz között. vagy ´te azt a hosszt érted valódinak, amit akkor mérünk, ha nyugalomban van?
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (18313):
Mit gondolsz, vajon miert nem tudsz senkit meggyozni arrol, hogy igazad lenne?Én csak elemeztem Einstein teóriáit, és levezettem azt, hogy a hibás részek miért hibásak.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (18313):
Mekkora a meresek hibaja, szorasa?Itt van például az alap, a gravitációs potenciál helyes értéke. Egyenlőre még nem íródott olyan levezetés amely 3-5 tizedes pontossággal megfelelne a fizikai mérésekben kapott értékeknek.
0 x
A relativitási elméletek
@vaskalapos (18944): Sajnos eléggé nagy ahhoz, hogy Einstein "jóslatától" való eltérés okát ne lehessen könnyen meghatározni.
Mint korábban említettem elvi hiba az ha a felszíni állandónak tekintett g értékével számol Einstein.
Miután a G értéke is energia potenciál függő, azaz a tömeg tehetetlenségi faktorával számolva kaphatnánk pontosabb értékeket, de mint a másik topicban éppen írtam, még a tehetetlenségi faktor is energia függő.
Azaz egy dologban mindenképpen igaza volt Einsteinnek: Szó szerint minden relatív, az állandók értéke is..
Mint korábban említettem elvi hiba az ha a felszíni állandónak tekintett g értékével számol Einstein.
Miután a G értéke is energia potenciál függő, azaz a tömeg tehetetlenségi faktorával számolva kaphatnánk pontosabb értékeket, de mint a másik topicban éppen írtam, még a tehetetlenségi faktor is energia függő.
Azaz egy dologban mindenképpen igaza volt Einsteinnek: Szó szerint minden relatív, az állandók értéke is..
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (18955):
Konkretan mekkora?
Lehet, hogy olyan nagy, hogy nem is lehet tudni, hogy van-e elteres, vagy csak a merese szorasa/hibaja okozza az elterest?
Konkretan mekkora?
Lehet, hogy olyan nagy, hogy nem is lehet tudni, hogy van-e elteres, vagy csak a merese szorasa/hibaja okozza az elterest?
0 x
A relativitási elméletek
@vaskalapos (18975): Amint tudjuk 1/R2 a távolság függés, ami az Einstein által használt felszíni g esetére R= 6 372 797 m
Ami a négyzetes hiperbola miatt az R=0 sugár felé közeledve erősen a végtelen nagyság felé kellene, hogy nőljön, távolodva pedig a végtelen R felé közel a zéróra csökken. Azaz nagyon nagy mértékű az eltérés "magasság" függése.
Ami a négyzetes hiperbola miatt az R=0 sugár felé közeledve erősen a végtelen nagyság felé kellene, hogy nőljön, távolodva pedig a végtelen R felé közel a zéróra csökken. Azaz nagyon nagy mértékű az eltérés "magasság" függése.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (18983):
Es Enstein a nulla es vegtelen sugar eseten is a felszini g-vel szamolt?
Szamomra ez hihetetlen.
Es Enstein a nulla es vegtelen sugar eseten is a felszini g-vel szamolt?
Szamomra ez hihetetlen.
0 x
A relativitási elméletek
@vaskalapos (18986): Igazából fel sem merült Einsteinnél a változás lehetősége amikor a gravitáció és az órák lassulása ( azaz a fénynek az energia és ezzel, ) az órajelet meghatározó frekvencia változását kapcsolta össze.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A relativitási elméletek
@Gézoo (18992): Pedig kozepiskolai tananyag, hogy a garvitacio tavolsaggal aranyosan (negyzetesen) valtozik.
Hogy nem gondolhatott erre?
Estleg idezned, konkretan mikor kovette el ezt a hibat?
Hogy nem gondolhatott erre?
Estleg idezned, konkretan mikor kovette el ezt a hibat?
0 x