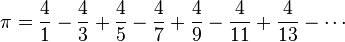@szemet (68914):
Érdekes eddig nem hallottam a Boltzmann-agyak problémájáról.
A dolog lényege, hogy a zárt rendszerek entrópiája monoton növekszik, míg eléri a maximális entrópiát, az ún. hőhalált. (Bár ez csak statisztikailag tekinthető igaznak.) Ha van egy rendszerünk, ami nagyon régi (esetleg végtelen ideje létezik), akkor az entrópiája törvényszerűen maximális, a legnagyobb rendezetlenségben van.
Amikor viszont körülnézünk, azt látjuk, hogy a világ körülöttünk határozottan tartalmaz rendezett struktúrákat, tehát nem lehet a mi világunk a hőhalál állapotában, pedig abban kéne lennie. Miért is nincs abban? Ez fogós ravasz kérdés.
A XIX.század végén, amikor az entrópia könyörtelen törvényeire rájöttek, csak egy dologra tudtak gondolni: mivel az entrópia statisztikai dolog, a maximális entrópiájú állapotban is ingadozik a rendszer, néha véletlenszerűen rendezettebbé válik egy kis térfogatában, majd újra tönkremegy ez a rendezettség. A valószínűségszámítás szerint az ilyen ingadozások közül a térfogatában és rendezettségében kisebb változások sokkal gyakoribbak azoknál, amelyek nagyobb térfogatot érintenek vagy jóval alacsonyabb entrópiát érnek el. Ez könnyen belátható. És erre vezethető vissza a Boltzmann-agyak problémája is. Melyik a valószínűbb statisztikai ingadozás: egy teljes univerzum felbukkanása milliárdnyi öntudatos agynak megfelelő alacsony entrópiával, vagy csupán egyetlen egy agynak megfelelő véletlen entrópiacsökkenés úgy, hogy az az egy agy pontosan olyan emlékeket tartalmaz, ami az "élet" érzetét okozza? Nyilvánvaló, hogy a második a valószínűbb, így ha igaz az entrópiára alapozott érvelés, és a valóság a hőhalál állapotában van, akkor valószínűbb, hogy te (én) ebben a pillanatban jött létre olyan emlékekkel, mintha leélte volna az életét eddig a pillanatig. (Az a szép ebben, hogy egy időben és térben végtelen hőhalál állapotú rendszerben minden megtörténik, azaz a te (én) agyállapot minden pillanata valahol és valamikor kialakul! Ha ezeket a külön állapotokat egymás mellé raknánk, akkor kijönne az a "történet", amit személyesen az életünknek érzékelünk.)
Viszont nem is nagyon értem a paradoxont, ugyanis a világ entrópiája akár lehet kisebb mint egy agyé (hiába van a világ tele agyakkal), esetleg van-e rá valami bizonyítékerejű számítás?
Lásd fent. A puszta statisztika. A világ en-bloc tényleg alacsonyabb entrópiájú, mint egy agy, éppen ezért valószínűtlenebb ingadozása egy hőhalál állapotában lévő rendszernek.
Az egész számok halmaza pl. kisebb entrópiájú mint egy véletlenül kiválasztott elegendően nagy egész szám.
Az entrópia egy kevéssé ismert megfogalmazása szerint a rendszer fázisterében adott tartomány térfogatának negatív logaritmusával arányos. (A megfogalmazás ekvivalens a statisztikai megfogalmazással.) Felmerül bennem a kérdés, hogy van-e fázistere az egész számoknak? Már itt kezdődnek a problémák az analógiáddal.
Jó hasonlat még az a kreacionista érv, hogy egy repülőgép nem áll össze az alkatrészekből véletlenül.
Összeáll. Csak nagyon-nagyon sok időbe telne.
Gyakorlatilag tekinthetjük lehetetlennek a 747-es roncstelepi összeállását. Ha pusztán csak az entrópia és a rendezettség oldaláról nézzük, akkor nemnulla a valószínűsége olyan ingadozásnak, ami éppen egy 747-est eredményez. Ennél természetesebben valószínűbb utat biztosít az összeszerelés (evolúció), ezért tekintjük azt a valószínűbbnek. De ekkor figyelmen kívül hagyjuk annak a valószínűségét, hogy a TELJES RENDSZER, amin belül a dolog megtörténik, mennyire is valószínűtlen egy hőhalál állapotában lévő rendszerből kiindulva. Mi a valószínűbb: egy darab 747-es felbukkanása a hőhalál rendezetlenségéből, vagy egy teljes univerzumnyi rendezett térfogat felbukkanása, amiben összeszerelhet egy intelligens lény egy 747-est? Ezért hiányos ez az analógia.
Pl. a PI képlete generálhatja a PI egymilliárd jegyét a számítógépemen, a véletlenszám generátor viszont nem nagyon. Azaz hihetőbb hogy a szabályos agyat egy szabályos gép generálta(pl. a világegyetem), minthogy magától így pattant elő.
Egyrészt a PI-nek nincs képlete. Irracionális szám az istenadta. Lehetnek algoritmusok, amelyek a PI számjegyeit kiadják neked, de ez az algoritmus pontosan végtelen ideig futna, ha a PI pontos értékét kérnéd tőle. Ez meg egy soha le nem álló Turing-gép lenne.
Másrészt most nem a "hihetőségen" hanem a "valószínűségen" van a hangsúly. Hogy én is egy analógiával világosítsam meg ezt: melyik a valószínűbb, hogy egy promóciós akcióban nyersz egy doboz sört, vagy hogy nyersz egy sörgyárat?
Mindezektől függetlenül természetesen a Boltzmann-agyak problémájának vannak más feloldásai, amik egyszerűen megkerülik a problémát. Például ha fizikai szabályt találunk arra, hogy az Ősrobbanás pillanatában csakis egy alacsony entrópiájú univerzum jöhet létre, akkor máris tárgytalanná válik az egész valószínűségekre alapozott hőhalálból kiinduló érvelés.
A magyar szólásokat sem ismered? Kirívó unintelligencia, vagy felrobbanhatsz az idegességtől, hogy még ezt sem tudod megfogalmazni. Segítek, az úgy van, hogy úgy táncol valaki, ahogy más fütyül.
gombbal lehet a moderátoroknak jelenteni és továbbítani.
Megmondom őszintén, most először kételkedek abban, amit írsz. Attól még, hogy valami végtelen, nem szükségszerű, hogy minden bekövetkezzen benne.
karaktert - a fogalom minden határon túli kiterjesztésével - "képletnek" nem tekintjük. Mert ugyanis ez az egy karakter az egyetlen, ami végtelen tizedesjegyre pontosan reprezentálja a pi értékét. És itt megint előkerül a kérdés: hogyan számolod ki a tizedesjegyes formáját?
