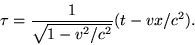Ha már a "c" jeltovábbítási sebesség és a "v" relatív sebesség ß=1/sin(arccos(v/c)) arányú, gammának nevezett mérési hiba arány szerint az egyik inerciális mozgású testhez rendelt koordináta rendszerből szemléltük a mérési hiba eredményét, akkor a relativitási elv értelmében a másik inerciális mozgású testhez rendelt koordináta rendszerből is illene leírnunk a hiba hatását.
Emlékeztetőül a topic-nyitó hozzászólásomban az ábra szereplő fényóra ábráján a v=0,8c relatív sebességgel haladó test hossza:
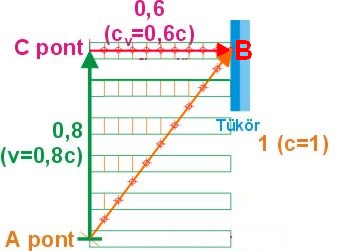
az adott elrendezésben a gamma ß=1/sin(arccos(v/c))=1/0,6 arányából következően, a valós hosszai helyett azoknak csupán 60%-os értékét mérhettük.
Ha viszont úgy szemléljük az ábrát, hogy a tükrös test rendszerében a C-B szakaszon cv helyett c sebességgel halad a c fénysebességű jeltovábbító jelenség, akkor az ugyanezen rendszerhez relatívan v=0,8c sebességgel mozgó és a jeltovábbító jelenség közötti távolodási sebesség c'=ß*c azaz
a narancs színű vektor irányában c'=1/sin(arccos(0,8/1))*c=1,67´c
Azaz ekkor a mérési hiba azt mutatja, hogy a v relatív sebességgel mozgóhoz viszonyított jeltovábbítási sebesség nagyobb a forrásától állandó c sebességgel távolodó fény sebességénél.
Igaz, ekkor nem a forrásától távolodik ekkora sebességgel a jeltovábbító jelenség, hanem a jel forrásától egyaránt távolodik v relatív sebességgel a mozgó és c relatív sebességgel a jeltovábbító jelenség, azaz a fény.
Ebből következően miután két, egymástól független mozgású "jelenség" egymástól független sebességgel mozog a tükrökhöz viszonyítva nyugvó testhez rendelt koordináta rendszerben, természetesen a fentebbi ok-okozat szabálya szerint, bármekkora relatív sebesség adódhat közöttük.
Mindebből viszont az következik, hogy a mérési elrendezés kiválasztásával, egyben a gamma azaz ß=1/sin(arccos(v/c)) arányú mérési hiba nem csak "rövidülésnek látszó", hanem a másik oldali elrendezés esetében "hosszabbodásnak látszó" mérési eredményt ad.
Ez a megállapítás pedig azért érdekes, mert a relativitási elv szerint, ha viszonyításnál az első tag kisebb a másodikhoz viszonyítva, akkor a logika szerint a második viszont nagyobb az elsőhöz viszonyítva, azaz:
Ha a < b akkor b > a , azaz teljesül a relativitási elv a gamma arányú mérési hiba alkalmazásakor is.
Persze az Einstein-féle relativitás teóriájában hívők, most felhorkanhatnának mondván, hogy:"A relativitási elv és az Einstein féle relativitás az két külön dolog!"
És ebben tökéletesen igazuk lenne. Miután az Einstein-féle változat nem teljesíti a relativitási elvet, bár kétségtelen mégis a relativitási elvre utaló nevet viseli.
Einstein teóriája félrevezető elnevezésnek mi lehetett az oka?
Talán nem nehéz választ adni erre a kérdésre ha elolvassuk az első sorait:
"ON THE ELECTRODYNAMICS OF MOVING BODIES
By A. Einstein, June 30, 1905
It is known that Maxwell's electrodynamics--as usually understood at the present time--when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. Take, for example, the reciprocal electrodynamic action of a magnet and a conductor. The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion. For if the magnet is in motion and the conductor at rest, there arises in the neighbourhood of the magnet an electric field with a certain definite energy, producing a current at the places where parts of the conductor are situated. But if the magnet is stationary and the conductor in motion, no electric field arises in the neighbourhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise--assuming equality of relative motion in the two cases discussed--to electric currents of the same path and intensity as those produced by the electric forces in the former case."
Azaz a Maxwell-féle elektrodinamikára próbált magyarázatot adni. Miután akkoriban nem volt indokolva az a jelenség, hogy amelyben mágneshez relatívan álló tekercsben nem keletkezik feszültség, de a mozgó tekercsben a mozgási sebesség nagyságával arányos nagyságú és a mozgási iránnyal változó előjelű feszültség képződik.
Einstein még nem tudhatott róla, de ma már tudjuk, hogy az univerzumunk két leggyakoribb részecskéjében a protonban és az elektronban is spinnel, ( magyarul perdülettel) rendelkező összetevők vannak. A protonokban a kvarkok, az elektronokban a holonok és a spinorok.
Valamint eddigi kísérleti tapasztalataink szerint, no és a mozgásokat leíró matematika szerint egyetlen perdület sem választható el a vele járó centripetális gyorsulástól.
Továbbá az is kísérleti tapasztalat, hogy minden gyorsulás (, még a centripetális gyorsulás is, ) a töltések esetében foton kisugárzástól sohasem mentes.
Ennek tudatában viszont nyilvánvaló, hogy bár sokféleképpen leírhatjuk az elektromos és/vagy mágneses mezőket, de minden leírásban a mező fénysebességű kiterjedési sebessége, azaz a fentebbi megfogalmazásaimban használt fénysebességű jeltovábbítási sebességgel rendelkező jelenségek.
Ezekből következően érvényes rájuk a gamma arányú "hiba". Azaz az ezen mezők-terek mérése során minden mérési eredményben benne lévő, a fentebb taglalt gamma ß=1/sin(arccos(v/c)) arányú mérési hiba megjelenése.
Ezen kísérleti tapasztalatok ismeretében viszont teljesen felesleges bevezetni Einstein teóriájának alkalmazását,
Maxwell elektrodinamikájának magyarázatára, hiszen a sokkal egyszerűbb magyarázattal megkapjuk a jelenség ok-okozati indoklását.
A mágnes és a tekercs közötti relatív mozgással az egyébként már a perdületük okán gyorsulás alatt álló töltéssel rendelkező részecskék fotonáramában történik a relatív mozgás.
Nyilvánvalóan ekkor a tekercsben lévő elektronokra
a "távolodó oldalról" E
-=E
0*((c-v)/(c+v)) foton energia hat,
a "közeledő oldalról" E
+=E
0*((c+v)/(c-v)) foton energia hat.
Ezen egyszerű relatív Doppler jelenség hatására az elektronokra E=E
+-E
- eredő foton energia hat.
Aminek hatására a kísérleti tapasztalatok szerint - -> + irányú elektron áramlás a következménye.
Természetesen a relatív mozgási irány megfordításakor felcserélődik a mágneshez viszonyított a távolodási és közeledési oldal, ezáltal az elektronokat mozgató eredő foton energia "polaritása" is megfordul.
Miután a kísérleti tapasztalatok szerint megmért elektromos feszültség nagysága és a relatív sebesség nagysága ugyanazon függvény szerinti eredményt adja, mint a rel.Dopplerrel kapott függvény, így kísérletileg igazolttá vált a felvázolt összefüggés.
Persze, természetesen, mint ahogy már korábban is emlékeztettem rá attól, hogy teljességgel felesleges Occam elve szerint az Einstein-féle relativitási teória, miután az alap kiindulási kérdése már egy nálánál lényegesen egyszerűbb kísérleti tapasztalattal tökéletesen igazolt elvvel is megválaszolható,
ettől még nyugodtan használhatja az aki szeret bonyolult, megalapozatlan elvek szerinti modelleket használni.
Miután az einstein-i modellből levezethető néhány eredmény, ( ha nem is mindegyik eredmény,) azonos a sokkal egyszerűbb modell szerint kapott eredményekkel.
No igen, de mi van az idő lassulásával? - tehetnénk fel a kérdést. Jogosan!
A fentiek ismeretében a válasz kézenfekvő:
Mint láttuk, a gamma azaz ß=1/sin(arccos(v/c)) arányú leolvasási, mérési hibát okoz a v relatív mozgási és és c relatív jeltovábbítási sebesség aránya minden v sebességű relatív mozgást végző testek esetében.
Ez természetesen nem csak a látott távolságok rövidülését vagy hosszabbodását érinti, hanem a jeltovábbítással "leolvasott" óra mutató állásokra is igaz. Miután ugyanazon leolvasási hiba fennáll.
Nyilvánvalóan gamma ß=1/sin(arccos(v/c)) arányú késéssel érkezik a jeltovábbító jelenség, akkor nem a realtime óraállást látjuk, hanem a korábbit.
Csupán annyi a különbség a hosszmérce leolvasása és az óraállás megfigyelése között, hogy amíg a hosszmérce mérési hibája csak a v relatív sebesség nagyságának ß=1/sin(arccos(v/c)) arányú függvénye, azaz időben állandó értékű, addig egy óra mutatóinak állása időben változó.
Így nyilvánvalóan ha van időfüggő komponense a jeltovábbításnak, akkor ezt a komponenst is bele kell tenni a hibát kompenzáló függvénybe.
Hogy mitől lenne idő függő az óra állás leolvasási hibája a ß=1/sin(arccos(v/c)) arány mellett?
Nos, egyszerű a válasz: a megfigyelési távolság meghatározza a jeltovábbítás idejét. Azaz egymástól x távolságra lévő, egyaránt v relatív sebességgel mozgó pontokon lévő óráktól:
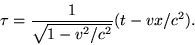
τ időkülönbséggel érkezik be a megfigyelőhöz az egymástól x távolságra lévő órák mutatóállását közvetítő jel továbbító jelenség, azaz a fény.
Azaz ezzel már nem csak ß=1/sin(arccos(v/c)) arányú leolvasási hibát követünk el, hanem kettős, a gamma és a távolság -> idő függő hibát is.
Természetesen ezzel azt a látszatot keltve a megfigyelőben, hogy a két megfigyelt óra állása (a megfigyelő saját órája szerinti) egy időpontban különböző.
Továbbá, miután az óra mutatóinak járása szerinti változást megszokásból, reflex szerűen azonosítjuk az idő múlásával, miután az óra mutatóinak járása alapvetően ennek az idő múlásának kijelzésére alkottattak, a megfigyelő tekintheti úgy is ezt a kettős leolvasási hibát,
mintha a megfigyelt test különböző pontjain "az idő" múlna különféle sebességgel.
Természetesen tudván, hogy az óra mutató állások, csak és kizárólag kettős leolvasási hibával figyelhetők meg, így ezzel a hibával kompenzálva leolvasott óra állásokat azt kapjuk, hogy a
megfigyelt v relatív sebességgel mozgó test minden pontján azonos járási sebességűek az óra mutatók.
Azaz az idő múlási sebességét, a kettős mérési hiba okozta látvány ellenére sem befolyásolja a relatív sebesség nagysága.
Azaz nem "az idő relatív", hanem az óramutató állások leolvasási hibájának nagysága relatív.
Ez a következmény ha igazolható, egyben feloldja azt a paradoxont, miszerint a szinkronozott órák mutatóinak egyformán kellene járnia, mégsem ezt figyelhetjük meg.
Vagyis a relatív egyidejűség elvének paradox tartalma ezáltal megszűnne.
Ó, igen. De hogyan lehetne azt igazolni, hogy egy megfigyelt v relatív sebességgel mozgó test minden pontján azonos sebességgel járnak az órák mutatói?
Nagyon egyszerűen. Minden óra mutatóit helyettesítsük egy-egy pl. idő etalonként használt sugárzóval.
Így ha az egyes pontokról a távolságtól függetlenül azonos frekvenciával érkezik be az időetalonok jele, akkor az órák mutatói a frekvenciával azonos járási sebességűen azonosak.
A mérési tapasztalat szerint, az egymáshoz relatívan nyugvó frekvencia etalonok jele egyforma relatív sebesség esetében, egyforma frekvencián mérhető, csak az eltérő mérési helyek távolságának függvényében, állandó sebesség esetén állandó mértékben a fázisaik térnek egymástól. Vagyis a "mutatók járási sebessége" azonos, csupán a fázisaik érzékelhetők különbözőnek.
Tehát ez sokszor megismételt megfigyelés igazolta azt, hogy a relatív egyidejűség távolság függő kettős hibája, valóban csupán megfigyelési hiba.
Ezzel a kettős hiba ok felderítéssel Occam elve szerint, Einstein teóriájának újabb "ágáról" derült ki, hogy felesleges tényezők bevezetésével magyarázta ugyanazt a jelenséget,
amit sokkal egyszerűbben is meg lehet magyarázni.. azaz Occam szerint elvetendő lenne.
A kettős hiba leírása, igazolása után, én igazából azokat sajnálom, akik az ezen kettős leolvasási hiba helyett úgy képzelték, hogy "időutazást" lehetne tenni, mert nem a leolvasási hiba a relatív, hanem maga az idő a relatív.
És ugye ha az idő és nem a leolvasási hiba lenne relatív, akkor akár téridőben is utazhattunk volna. Féregjáratokkal, csillagkapukkal legyőzhettük volna a végtelen távolságok adta korlátokat.