A tudományos parapszichológiáról (a blog kapcsán)
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
A tudományos parapszichológiáról (alcime: kísérleti eredmények a múltból és a jelenből) cimu
Blogbejegyzes kommentjeit a Blog Moderatora zarolta.
Szerintem erdemes lenne itt folytatni az eszmecseret a szignifikancia szintekrol, az elfogultsagrol, anekdotak bizonyito erejerol (vagy annak hianyarol).
Kiindulas a fentebb citalt Blogbejegyzes, annak kommentjei es az ott elolvasasra javasolt Vassy fele kezirat, Materialista parapszichologia.
Kicsit nehezkes a kezelese a keziratnak, de megeri letolteni, nagyon erdekes, es jo bepillantast nyujt a tudomanyos ezoteriaba.
Telepatia, tavolbalatas, ismeretlen informaciok megszerzese mentalis uton, jovobelatas, joslas (pl tozsde vagy kaszino) es sok mas erdekesseg, anekdotak es tudomanyosnak tuno szamolasok erdekes kevereke.
Blogbejegyzes kommentjeit a Blog Moderatora zarolta.
Szerintem erdemes lenne itt folytatni az eszmecseret a szignifikancia szintekrol, az elfogultsagrol, anekdotak bizonyito erejerol (vagy annak hianyarol).
Kiindulas a fentebb citalt Blogbejegyzes, annak kommentjei es az ott elolvasasra javasolt Vassy fele kezirat, Materialista parapszichologia.
Kicsit nehezkes a kezelese a keziratnak, de megeri letolteni, nagyon erdekes, es jo bepillantast nyujt a tudomanyos ezoteriaba.
Telepatia, tavolbalatas, ismeretlen informaciok megszerzese mentalis uton, jovobelatas, joslas (pl tozsde vagy kaszino) es sok mas erdekesseg, anekdotak es tudomanyosnak tuno szamolasok erdekes kevereke.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@vaskalapos (39915):
Akartam irni a one-tail es a two tail teszthez valamit, erre be volt zarolva a tema. Orulok, hogy itt egy ujabb nyilott.
En ugy tanultam, ha van feltetelezesem, hogy milyen iranyban fognak elterni az adataim mondjuk egy kezeles hatasara, tehat ha mar van egy priori hipotezisem, arra eleg a one tail teszt. Ha viszont nem tudom, hogy merre fognak elterni az adataim, vagy nem fognak valtozni az adataim a kezeles hatasara, akkor szigorubb, two tail tesztet kell hasznalni.
Itt alabb kicsit maskepp magyarazza, de ez is erdekes.
http://www.statpac.com/surveys/statisti ... icance.htm
Akartam irni a one-tail es a two tail teszthez valamit, erre be volt zarolva a tema. Orulok, hogy itt egy ujabb nyilott.
En ugy tanultam, ha van feltetelezesem, hogy milyen iranyban fognak elterni az adataim mondjuk egy kezeles hatasara, tehat ha mar van egy priori hipotezisem, arra eleg a one tail teszt. Ha viszont nem tudom, hogy merre fognak elterni az adataim, vagy nem fognak valtozni az adataim a kezeles hatasara, akkor szigorubb, two tail tesztet kell hasznalni.
Itt alabb kicsit maskepp magyarazza, de ez is erdekes.
http://www.statpac.com/surveys/statisti ... icance.htm
One-Tailed and Two-Tailed Significance
Tests
One important concept in significance testing is
whether you use a one-tailed or two-tailed test of
significance. The answer is that it depends on your
hypothesis. When your research hypothesis states the
direction of the difference or relationship, then you use
a one-tailed probability. For example, a one-tailed test
would be used to test these null hypotheses: Females will
not score significantly higher than males on an IQ test.
Blue collar workers are will not buy significantly more
product than white collar workers. Superman is not
significantly stronger than the average person. In each
case, the null hypothesis (indirectly) predicts the
direction of the difference. A two-tailed test would be
used to test these null hypotheses: There will be no
significant difference in IQ scores between males and
females. There will be no significant difference in the
amount of product purchased between blue collar and white
collar workers. There is no significant difference in
strength between Superman and the average person. The
one-tailed probability is exactly half the value of the
two-tailed probability.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
Kíváncsi vagyok a véleményetekre.
Nem sokkal a zárás előtt szóltam hozzá és azt kérdeztem, miért nem lehet olyan kísérletet összeállítani, amelynél nem szükséges 5%-os valószínűségekkel bűvészkedni.
Kérlek olvassátok el sztrugackij(én vagyok) és fordulóbogyó utolsó néhány hozzászólását/2012.01.24 19:42/, hogy egyáltalán jól értelmeztem-e a dolgokat.
Köszönöm.
Nem sokkal a zárás előtt szóltam hozzá és azt kérdeztem, miért nem lehet olyan kísérletet összeállítani, amelynél nem szükséges 5%-os valószínűségekkel bűvészkedni.
Kérlek olvassátok el sztrugackij(én vagyok) és fordulóbogyó utolsó néhány hozzászólását/2012.01.24 19:42/, hogy egyáltalán jól értelmeztem-e a dolgokat.
Köszönöm.
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@lorenz (39925):
Egy véletlenszerű zavaró tényezőt biztosan kiszűrni végtelen számú kísérlettel lehet. Ez nem kivitelezhető. Végzünk hát sokat, de nem végtelent. A véletlenszerű zavaró tényező lényege, hogy véletlenszerű! Emiatt lehet, hogy a véges számú kísérletünk során nem a feltételezett eloszlása szerint oszlott meg a hatása ("úgy esett, hogy mindig fejet dobtunk"). Ezért csak azt mondhatjuk, hogy mennyire valószínű az, hogy a kapott eredményt a vak véletlen produkálta. Például, 5% alatti az esélye. Ami azt jelenti, hogy ha az adott kísérletsorozatot végtelenszer megismételnénk (amikoris tehát a véletlenszerű zavaró tényező biztosan kiesik), akkor átlagosan (aszimptotikusan közeledve) az esetek 5%-ában fogjuk csak azt az eredményt kapni, amit az egy kísérletsorozat végén kaptunk.
Emiatt lehet, hogy a véges számú kísérletünk során nem a feltételezett eloszlása szerint oszlott meg a hatása ("úgy esett, hogy mindig fejet dobtunk"). Ezért csak azt mondhatjuk, hogy mennyire valószínű az, hogy a kapott eredményt a vak véletlen produkálta. Például, 5% alatti az esélye. Ami azt jelenti, hogy ha az adott kísérletsorozatot végtelenszer megismételnénk (amikoris tehát a véletlenszerű zavaró tényező biztosan kiesik), akkor átlagosan (aszimptotikusan közeledve) az esetek 5%-ában fogjuk csak azt az eredményt kapni, amit az egy kísérletsorozat végén kaptunk.
Nem lehet megúszni statisztika nélkül.
Legegyszerűbb példa talán az enyhén cinkelt érme. Hogyan állapítanád meg, hogy tökéletesen szimmetrikus-e, vagy egy leheletnyivel többször ad fejet?
A (vélt) hatás gyenge. Ha gyenge, akkor 1-2 kísérlet nem ad meggyőző bizonyítékot. Ha sok kísérlet kell, akkor ezek eredményét valamilyen módon összesítve kell kiértékelni. Megérkeztünk a statisztikához.Nem sokkal a zárás előtt szóltam hozzá és azt kérdeztem, miért nem lehet olyan kísérletet összeállítani, amelynél nem szükséges 5%-os valószínűségekkel bűvészkedni.
Egy véletlenszerű zavaró tényezőt biztosan kiszűrni végtelen számú kísérlettel lehet. Ez nem kivitelezhető. Végzünk hát sokat, de nem végtelent. A véletlenszerű zavaró tényező lényege, hogy véletlenszerű!
Nem lehet megúszni statisztika nélkül.
Legegyszerűbb példa talán az enyhén cinkelt érme. Hogyan állapítanád meg, hogy tökéletesen szimmetrikus-e, vagy egy leheletnyivel többször ad fejet?
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@lorenz (39925):
Ugy velem ez nem a kiserlet tervezesen mulik, hanem a vizsgalt jelensegen.
ha egy jelenseg kontrollalt korulmenyek kozott jol megismetelheto, reprodukalhato, akkor kiserleti osszeallitastol fuggetlenul azt tapasztaljuk.
Peldanak itt van ket-harom kiserlet.
Az elso egy hagyomanyos vizsgalat. Olyan, mint a szemorvosnal. Egy betut vetitesz az ernyore es a kiserleti alany megmondja, hogy melyik betut latja.
Igy lehet tesztelni, hogy lat-e, sot azt is, hogy milyen tavolsagbol latja meg elegendo elesseggel...
A kiertekeles egyszeru: ha latja, akkor azt betut nevezi meg, amit vetitunk, ha mas betut nevez meg, akkor nem latja (vagy nem eleg elesen).
Ugye ha talalgat, az hamar kiderul, mert harmincvalahany betubol egyet eltalalni az esely egy a harmicvalahanyhoz, azaz kb 3%. Szaz probabol atlagosan 97-szer fog tevedni.
Ennek egy valtozata legyen a mi kiserletunk, feldobunk egy ermet, amikor leesik, akkor a kiserleti alany megmondja, fej vagy iras amit lat.
Ez mar erdekesebb. Ha latja, akkor ugye kozel 100%-ban helyesen valaszol (kiveve, amikor elbambul, veletlenul mast mond, mint amit lat stb).
De ha egyaltalan nem latja, es megis mond valamit, akkor is ugy atlagosan az esetek feleben eltalalja, hogy fej, vagy iras volt felul.
A masik kiserletben az egyik szobaban dobaljak a penzermet es a masik szobaban levo kiserleti alanyt kerdezik, hogy mi a dobas eredmenye.
A harmadik kiserletben holnap fogjak a penzermet dobalni, de a kiserleti alany most mondja meg, mi lesz az eredmeny.
Ezekben a kiserletekben is kozel 100 szazalekos talalatot varunk, ha valoban "lat" a tavolba vagy a jovobe a kiserleti alany. Ha meg egyaltalan nem lat, csak talalgat, akkor 50% koruli eredmenyre szamitunk.
A kiserleti elrendezes ugyanaz.
Nagyon jo kerdes.Nem sokkal a zárás előtt szóltam hozzá és azt kérdeztem, miért nem lehet olyan kísérletet összeállítani, amelynél nem szükséges 5%-os valószínűségekkel bűvészkedni.
Ugy velem ez nem a kiserlet tervezesen mulik, hanem a vizsgalt jelensegen.
ha egy jelenseg kontrollalt korulmenyek kozott jol megismetelheto, reprodukalhato, akkor kiserleti osszeallitastol fuggetlenul azt tapasztaljuk.
Peldanak itt van ket-harom kiserlet.
Az elso egy hagyomanyos vizsgalat. Olyan, mint a szemorvosnal. Egy betut vetitesz az ernyore es a kiserleti alany megmondja, hogy melyik betut latja.
Igy lehet tesztelni, hogy lat-e, sot azt is, hogy milyen tavolsagbol latja meg elegendo elesseggel...
A kiertekeles egyszeru: ha latja, akkor azt betut nevezi meg, amit vetitunk, ha mas betut nevez meg, akkor nem latja (vagy nem eleg elesen).
Ugye ha talalgat, az hamar kiderul, mert harmincvalahany betubol egyet eltalalni az esely egy a harmicvalahanyhoz, azaz kb 3%. Szaz probabol atlagosan 97-szer fog tevedni.
Ennek egy valtozata legyen a mi kiserletunk, feldobunk egy ermet, amikor leesik, akkor a kiserleti alany megmondja, fej vagy iras amit lat.
Ez mar erdekesebb. Ha latja, akkor ugye kozel 100%-ban helyesen valaszol (kiveve, amikor elbambul, veletlenul mast mond, mint amit lat stb).
De ha egyaltalan nem latja, es megis mond valamit, akkor is ugy atlagosan az esetek feleben eltalalja, hogy fej, vagy iras volt felul.
A masik kiserletben az egyik szobaban dobaljak a penzermet es a masik szobaban levo kiserleti alanyt kerdezik, hogy mi a dobas eredmenye.
A harmadik kiserletben holnap fogjak a penzermet dobalni, de a kiserleti alany most mondja meg, mi lesz az eredmeny.
Ezekben a kiserletekben is kozel 100 szazalekos talalatot varunk, ha valoban "lat" a tavolba vagy a jovobe a kiserleti alany. Ha meg egyaltalan nem lat, csak talalgat, akkor 50% koruli eredmenyre szamitunk.
A kiserleti elrendezes ugyanaz.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (39931):
Tudnal par peldat hozni a tudomanybol, ahol ilyen gyenge hatast vizsgalnak?A (vélt) hatás gyenge. Ha gyenge, akkor 1-2 kísérlet nem ad meggyőző bizonyítékot.
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@vaskalapos (39933):
Általánosságban minden nem elég jól modellezhető/modellezett, bonyolult rendszer esetén a rendszernek adott input és a rá adott válasz közti korreláció keresésekor előfordulnak megkérdőjelezhető, nagyon áttételes hatásmechanizmusok, s emiatt igen gyenge hatások. Orvoslás, szociológia, pszichológia, gazdaság.
Ha nem bonyolult rendszereket nézzük, akkor jobb úgy feltenni a kérdést a tisztánlátás végett, hogy hol van nagyon nagy zaj a vizsgált (feltételezett) jelenség jelszintjéhez képest? Itt elég jól szerepel az asztrofizika. Kimérni olyan távoli égitestek fényét, melyet közben kismillió köd, csillag, mifene perturbál. Vagy a gravitációs hullámok keresése. Bazipontos mérések szükségesek, azokból is nagyon sok, és akkor keressük a számtengerben a várt, zajból kicsit kiemelkedő mintákat.
Az orvostudományban hemzseg, de ezt te nyilván jobban tudod. Pl. milyen ételeknek, életmódnak, környezeti hatásoknak van rák kockázati tényezőt növelő hatása.Tudnal par peldat hozni a tudomanybol, ahol ilyen gyenge hatast vizsgalnak?
Általánosságban minden nem elég jól modellezhető/modellezett, bonyolult rendszer esetén a rendszernek adott input és a rá adott válasz közti korreláció keresésekor előfordulnak megkérdőjelezhető, nagyon áttételes hatásmechanizmusok, s emiatt igen gyenge hatások. Orvoslás, szociológia, pszichológia, gazdaság.
Ha nem bonyolult rendszereket nézzük, akkor jobb úgy feltenni a kérdést a tisztánlátás végett, hogy hol van nagyon nagy zaj a vizsgált (feltételezett) jelenség jelszintjéhez képest? Itt elég jól szerepel az asztrofizika. Kimérni olyan távoli égitestek fényét, melyet közben kismillió köd, csillag, mifene perturbál. Vagy a gravitációs hullámok keresése. Bazipontos mérések szükségesek, azokból is nagyon sok, és akkor keressük a számtengerben a várt, zajból kicsit kiemelkedő mintákat.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@lorenz (39925):
Ugy velem, 5% az altalanosan elfogadott szignifikancia szint (p < 0.05), azaz amikor a vizsgalt esemeny elofordulasa nem veletlenszeru. De ezt lehet szigoritani pl. 1%-ra szukiteni (p < 0.01), vagy 10%-ra emelni (bar az szerintem csak tendencia).
Sok tudomanyos cikkben, ha valami szignifikansnak jon ki, akkor meg azt is odairjak, hogy p < 0.0001. Tulajdonkeppen ez szuksegtelen, mert ha p < 0.05 a kriterium, akkor ami alatta van az is szignifikansan eltero. Nekem mintha ezt magyarazta volna a statisztika tanar. Kepletekkel sajnos nem tudok ervelni.
Ugy velem, 5% az altalanosan elfogadott szignifikancia szint (p < 0.05), azaz amikor a vizsgalt esemeny elofordulasa nem veletlenszeru. De ezt lehet szigoritani pl. 1%-ra szukiteni (p < 0.01), vagy 10%-ra emelni (bar az szerintem csak tendencia).
Sok tudomanyos cikkben, ha valami szignifikansnak jon ki, akkor meg azt is odairjak, hogy p < 0.0001. Tulajdonkeppen ez szuksegtelen, mert ha p < 0.05 a kriterium, akkor ami alatta van az is szignifikansan eltero. Nekem mintha ezt magyarazta volna a statisztika tanar. Kepletekkel sajnos nem tudok ervelni.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (39936): Valami konkretabbat nem tudsz?
Az orvostudomanyban, eletmod vagy taplalkozastudomanyban szerintem kinevetnek, ha azzal jossz, hogy valami szignifikansan 3%-kal noveli a valaminek az elofordulasat.
A parapszichologusok (vagy minek nevezik a tema kutatoi magukat?) meg 80 eve kutatnak olyan jelensegeket, amik a veletlentol sokszor meg 3%-kal sem ternek el.
Az orvostudomanyban, eletmod vagy taplalkozastudomanyban szerintem kinevetnek, ha azzal jossz, hogy valami szignifikansan 3%-kal noveli a valaminek az elofordulasat.
A parapszichologusok (vagy minek nevezik a tema kutatoi magukat?) meg 80 eve kutatnak olyan jelensegeket, amik a veletlentol sokszor meg 3%-kal sem ternek el.
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@vaskalapos (39939): Ha jól értem, azt igyekszel a sorok között kifejezni, hogy a parapszichológia (tudományos irányzata is) csak harmatgyenge erőlködés más tudományos kutatásokhoz eredményeihez képest. Ezt kimondhatod így kerek-perec is, ugyanígy gondolom én is.
A múltkori előadás után bennem ez úgy fogalmazódott meg, hogy amíg azon megy az iszapbirkózás, hogy tudunk-e olyan statisztikai módszert találni, olyan metanalízist készíteni, amiben végre megvillan a szignifikancia, addig ez egy szánalmas vicc.
A múltkori előadás után bennem ez úgy fogalmazódott meg, hogy amíg azon megy az iszapbirkózás, hogy tudunk-e olyan statisztikai módszert találni, olyan metanalízist készíteni, amiben végre megvillan a szignifikancia, addig ez egy szánalmas vicc.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@Orcas (39937):
p < 0.05 azt jelnti, hogy kisebb mint 5% a valoszinusege annak, hogy a nullhipotezis megis igaz (azaz az eredmeny teves)Ugy velem, 5% az altalanosan elfogadott szignifikancia szint (p < 0.05), azaz amikor a vizsgalt esemeny elofordulasa nem veletlenszeru
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (39940):
Nem, nem pont igy gondolom. Inkabb ugy, hogy elfogult, es eloiteleteit (pszi letezik, telepatia letezik, jovobelatas letezik) nem hajlando feladni, annak ellenere, hogy meggyozoen bizonyitani sem tudja.Ha jól értem, azt igyekszel a sorok között kifejezni, hogy a parapszichológia (tudományos irányzata is) csak harmatgyenge erőlködés más tudományos kutatásokhoz eredményeihez képest. Ezt kimondhatod így kerek-perec is, ugyanígy gondolom én is.
Statisztikailag lehet szignifikans akar p<0.001 szinten is, ha a veletlen talalgatastol valo elteres ilyen kicsi, es nem reprodukalhato, akkor vicc az egesz.A múltkori előadás után bennem ez úgy fogalmazódott meg, hogy amíg azon megy az iszapbirkózás, hogy tudunk-e olyan statisztikai módszert találni, olyan metanalízist készíteni, amiben végre megvillan a szignifikancia, addig ez egy szánalmas vicc.
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@vaskalapos (39942):
OK, ezzel is egyetértek.Inkabb ugy, hogy elfogult, es eloiteleteit (pszi letezik, telepatia letezik, jovobelatas letezik) nem hajlando feladni, annak ellenere, hogy meggyozoen bizonyitani sem tudja.
Ja. Nekem András velős felszólalása tetszett, hogy ti. metaanalízisből sem csak egy van, hanem az egyik kihoz eltérést a zajtól, a másik nem. Lehet válogatni. Számomra ez innentől vicc. Ha létezik is a hatás, de olyan kicsi, hogy a módszerválasztással kell erőlködni, hogy ez kijöjjön, akkor vagy nagyon rossz kísérleteket eszelnek ki, vagy irrelevánsan kicsi a dolog jelentősége.Statisztikailag lehet szignifikans akar p<0.001 szinten is, ha a veletlen talalgatastol valo elteres ilyen kicsi, es nem reprodukalhato, akkor vicc az egesz.
0 x
-
Szilágyi András
- *

- Hozzászólások: 6523
- Csatlakozott: 2009.12.05. 09:31
- Tartózkodási hely: Budapest
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (39943):
A helyzet ennél jóval összetettebb. Ganzfeld vizsgálatokról legalább 5 metaanalízis van, ezek közül csak egy negatív, az összes többi pozitív eredményű. Nem egy időpontban készültek és más-más adathalmazon alapulnak. A negatív eredményű 1999-es.
Ez viszont egy 2010-es elemzés táblázata, ami 56 egyedi vizsgálat adatait tartalmazza:
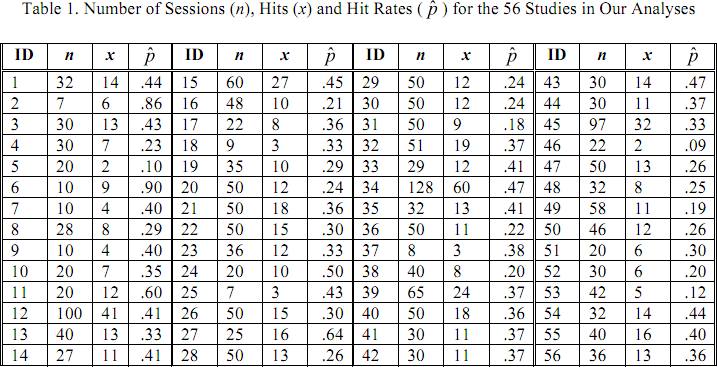
Ez mind a szokásos 4 cél közül választós kísérlet volt, tehát a várható találati arány 25% volt. A táblázat alapján az összesített találati arány 33,4%, egyvégű egzakt binomiális teszt alapján P=2,26·10-18.
Egyébként újraelemezték az 1999-es negatív eredményű metaanalízist is, akkoriban még nem csináltak egzakt binomiális tesztet. Egzakt binomiális teszttel arra az adathalmazra az összesített találati arány 27%, P=0,03, tehát valójában az is szignifikáns.
A helyzet ennél jóval összetettebb. Ganzfeld vizsgálatokról legalább 5 metaanalízis van, ezek közül csak egy negatív, az összes többi pozitív eredményű. Nem egy időpontban készültek és más-más adathalmazon alapulnak. A negatív eredményű 1999-es.
Ez viszont egy 2010-es elemzés táblázata, ami 56 egyedi vizsgálat adatait tartalmazza:
Ez mind a szokásos 4 cél közül választós kísérlet volt, tehát a várható találati arány 25% volt. A táblázat alapján az összesített találati arány 33,4%, egyvégű egzakt binomiális teszt alapján P=2,26·10-18.
Egyébként újraelemezték az 1999-es negatív eredményű metaanalízist is, akkoriban még nem csináltak egzakt binomiális tesztet. Egzakt binomiális teszttel arra az adathalmazra az összesített találati arány 27%, P=0,03, tehát valójában az is szignifikáns.
0 x
-
Szilágyi András
- *

- Hozzászólások: 6523
- Csatlakozott: 2009.12.05. 09:31
- Tartózkodási hely: Budapest
A tudományos parapszichológiáról (a blog kapcsán)
@vaskalapos (39941): Nem, nem azt jelenti. A P érték nem a nullhipotézis valószínűsége az adatok ismeretében, hanem az adatok valószínűsége, ha a nullhipotézis igaz.
A nullhipotézis valószínűségét a Bayes-képlettel számolhatod ki, ahhoz viszont meg kell adnod a nullhipotézis a priori valószínűségét.
A nullhipotézis valószínűségét a Bayes-képlettel számolhatod ki, ahhoz viszont meg kell adnod a nullhipotézis a priori valószínűségét.
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@Szilágyi András (39944): Nos jó. Ez esetben azt mondanám, ha egy ismerősöm jönne ilyen eredményekkel, hogy szóljon majd akkor ha sikerül tisztítani a kísérleteken. Legyen legalább egy olyan paraméter, mely megbízható korrelációt mutat az eredményességgel.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (39943):
Eredmeny: nulla.
Jobbnal jobb kiserleteket eszelnek ki, neha talalnak a veletlen talalgatastol szignifikans elterest (ez csak annyit jelent, hogy olyan esemenysorozatokba is belefutnak, amiknek a valoszinusege kisebb, mint 5%), de semmi elorelepes, semmi valtozas.
Ha belegondolsz, hogy valoban letezo jelensegekre micsoda tudomanyos es technologiai fejlodest lattunk akar csak az elmult 20 evben, akkor egyertelmu kell legyen, hogy a jelenseg nem letezik, azert nincs elorelepes.
Pedig lenne ra igeny, a politikaban, a gazdasagban, a hirszerzesben, az informaciotovabbitasban stb stb szamtalan felhasznalasa lenetne.
Termeszetesen valaminek a nemletet nem lehet bizonyitani, igy az idok vegezeteik lehet jatszani, hatha egyszer megis talalnak erzeken tuli eszlelest, jovobelatast, meg hasonlokat.
Azt hiszem, az 1 millio dollaros Randi fele dij is ervenyes lenne ezekre a jelensegekre is. Nem palyaznak... ok tudjak, miert. En csak sejtem.
Ennel egyertelmubb a helyzet szerintem. A jelenseget mar nagyon regen felteteleztek (remeltek, hittek) es legalabb 80 eve tudomanyosan is probaljak kutatni.Ha létezik is a hatás, de olyan kicsi, hogy a módszerválasztással kell erőlködni, hogy ez kijöjjön, akkor vagy nagyon rossz kísérleteket eszelnek ki, vagy irrelevánsan kicsi a dolog jelentősége.
Eredmeny: nulla.
Jobbnal jobb kiserleteket eszelnek ki, neha talalnak a veletlen talalgatastol szignifikans elterest (ez csak annyit jelent, hogy olyan esemenysorozatokba is belefutnak, amiknek a valoszinusege kisebb, mint 5%), de semmi elorelepes, semmi valtozas.
Ha belegondolsz, hogy valoban letezo jelensegekre micsoda tudomanyos es technologiai fejlodest lattunk akar csak az elmult 20 evben, akkor egyertelmu kell legyen, hogy a jelenseg nem letezik, azert nincs elorelepes.
Pedig lenne ra igeny, a politikaban, a gazdasagban, a hirszerzesben, az informaciotovabbitasban stb stb szamtalan felhasznalasa lenetne.
Termeszetesen valaminek a nemletet nem lehet bizonyitani, igy az idok vegezeteik lehet jatszani, hatha egyszer megis talalnak erzeken tuli eszlelest, jovobelatast, meg hasonlokat.
Azt hiszem, az 1 millio dollaros Randi fele dij is ervenyes lenne ezekre a jelensegekre is. Nem palyaznak... ok tudjak, miert. En csak sejtem.
A hozzászólást 1 alkalommal szerkesztették, utoljára vaskalapos 2012.02.02. 01:42-kor.
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@Szilágyi András (39945):
OK 100% szamold ki igy legyszi, a p<0.05-re
A gondolatetvitel (egymassal semmifele ismert fizikai kapcsolatban nem levo emberek kozti informacioatvitel) a priori nem letezik. 100%
Konkreten adjam meg a valoszinuseget annak, hogy jovobelatas a priori nem letezik?ahhoz viszont meg kell adnod a nullhipotézis a priori valószínűségét
OK 100% szamold ki igy legyszi, a p<0.05-re
A gondolatetvitel (egymassal semmifele ismert fizikai kapcsolatban nem levo emberek kozti informacioatvitel) a priori nem letezik. 100%
0 x
-
vaskalapos
- Hozzászólások: 4606
- Csatlakozott: 2009.12.09. 17:51
A tudományos parapszichológiáról (a blog kapcsán)
@Szilágyi András (39944):
Andras, ha megengedsz egy szemelyes kerdest (termeszetesen semmi kozom hozza, ne erezd, hogy valaszolnod kell, de ha megis valaszolsz, nagyra ertekelnem):
Hogyan egyeztetheto ossze felvallalt szkeptikussagoddal, es a Tarsasagban valo vezeto szerepeddel a parapszichologia ilyenten kvazi elismerese?
Ilyen kriteriumok alapjan az osszes altudomany, az iriszdiagnosztikatol a bizorezonanciaig, a homeopatian at a kapcsolatteremto gyogyitasig es az asztrologiaig, mind elfogadhato lenne.
Van, hogy a veletlennel kicsit jobban teljesitenek ezek is, nem?
Andras, ha megengedsz egy szemelyes kerdest (termeszetesen semmi kozom hozza, ne erezd, hogy valaszolnod kell, de ha megis valaszolsz, nagyra ertekelnem):
Hogyan egyeztetheto ossze felvallalt szkeptikussagoddal, es a Tarsasagban valo vezeto szerepeddel a parapszichologia ilyenten kvazi elismerese?
Ilyen kriteriumok alapjan az osszes altudomany, az iriszdiagnosztikatol a bizorezonanciaig, a homeopatian at a kapcsolatteremto gyogyitasig es az asztrologiaig, mind elfogadhato lenne.
Van, hogy a veletlennel kicsit jobban teljesitenek ezek is, nem?
0 x
-
Szilágyi András
- *

- Hozzászólások: 6523
- Csatlakozott: 2009.12.05. 09:31
- Tartózkodási hely: Budapest
A tudományos parapszichológiáról (a blog kapcsán)
Szerintem vaskalapos úr már eleget hangoztatta a véleményét ebben a témában.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@vaskalapos (39949): Mivel magyarazza azt, hogy a Ganzfeld kiserletek nem csak neha, hanem altalaban 35% talalati aranyt adnak?
0 x
A tudományos parapszichológiáról (a blog kapcsán)
http://index.hu/tudomany/2013/04/04/gon ... ny_farkat/
http://www.newscientist.com/article/dn2 ... -move.html
Az emberi agy EKG hullamait egy szamitogep ertekelte, ki tudta szurni az EKG zajbol, hogy mikor akart az ember patkanyfarkot mozgatni (miutan a kiserleti alanyok megtanultak, begyakoroltak, hogyan valtoztassak ez EKG jeluket), es akkor bekapcsolta az ultrahangot a patkany fejen.
http://www.plos.org/media/press/2013/pone-08-04-yoo.pdf
Non-Invasive Brain-to-Brain Interface (BBI): Establishing Functional Links between Two Brains
90% folotti sikerrel mukodott, es atlagban 1.5 masodperc alatt atment az informacio, a ragondolast kovetoen ennyi idovel mozdult a farok.
Irja az INDEX.Egy lépéssel közelebb kerültek a kutatók ahhoz, hogy megértsék a telepátiát. Egy új kísérletsorozattal sikerült elérni, hogy az emberek gondolataikkal mozgásra késztessék patkányok farkát.
http://www.newscientist.com/article/dn2 ... -move.html
Nem az emberi gondolat, hanem gepi ultrahang impulzus hatott a patkany agyara, attol mozgott a farka.an anaesthetised rat was hooked up to a device that made the creature's neurons fire whenever it delivered an ultrasonic pulse to the rat's motor cortex.
Itt bizony ossze volt huzalozva az ember es a patkany feje.Telepathy is the transmission of information from one person to another without using any of our known sensory channels or physical interaction.
Az emberi agy EKG hullamait egy szamitogep ertekelte, ki tudta szurni az EKG zajbol, hogy mikor akart az ember patkanyfarkot mozgatni (miutan a kiserleti alanyok megtanultak, begyakoroltak, hogyan valtoztassak ez EKG jeluket), es akkor bekapcsolta az ultrahangot a patkany fejen.
http://www.plos.org/media/press/2013/pone-08-04-yoo.pdf
Non-Invasive Brain-to-Brain Interface (BBI): Establishing Functional Links between Two Brains
azert ez maskent hangzik, mint a bulvarsajto hireTranscranial focused ultrasound (FUS) is capable of modulating the neural activity of specific brain regions, with a potential
role as a non-invasive computer-to-brain interface (CBI). In conjunction with the use of brain-to-computer interface (BCI)
techniques that translate brain function to generate computer commands, we investigated the feasibility of using the FUSbased CBI to non-invasively establish a functional link between the brains of different species (i.e. human and SpragueDawley rat), thus creating a brain-to-brain interface (BBI). The implementation was aimed to non-invasively translate the
human volunteer’s intention to stimulate a rat’s brain motor area that is responsible for the tail movement. The volunteer
initiated the intention by looking at a strobe light flicker on a computer display, and the degree of synchronization in the
electroencephalographic steady-state-visual-evoked-potentials (SSVEP) with respect to the strobe frequency was analyzed
using a computer. Increased signal amplitude in the SSVEP, indicating the volunteer’s intention, triggered the delivery of
a burst-mode FUS (350 kHz ultrasound frequency, tone burst duration of 0.5 ms, pulse repetition frequency of 1 kHz, given
for 300 msec duration) to excite the motor area of an anesthetized rat transcranially. The successful excitation subsequently
elicited the tail movement, which was detected by a motion sensor.
90% folotti sikerrel mukodott, es atlagban 1.5 masodperc alatt atment az informacio, a ragondolast kovetoen ennyi idovel mozdult a farok.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
Milyen szerencse, hogy nem létezik a gondolatátvitel! Tudnillik akkor villamoson, buszon, emberek csoportosulásában nem lehetne gondolkodni. Egymás gondolatai úgy összezavarnák az agyakat, hogy tökéletes tohuvabohu állna elő.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@Vaszilov (67858):
Az ESP topikban olvasd a vitat
Nincs mindenki meggyozodve arrol, hogy nem letezik a gondolatatvitel.
Azzal ervelnek, hogy nagyon-nagyon gyenge hatasa.
De statisztikailag szignifikans.
Az ESP topikban olvasd a vitat
Nincs mindenki meggyozodve arrol, hogy nem letezik a gondolatatvitel.
Azzal ervelnek, hogy nagyon-nagyon gyenge hatasa.
De statisztikailag szignifikans.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@ennyi (67861):
Elolvastam az utolsó oldalt, de nincs kedvem bekapcsolódni.
A témával kapcsolatos véleményemet itt olvashat(tad)-od:
http://file1.npage.de/001876/61/html/alf55.html
Elolvastam az utolsó oldalt, de nincs kedvem bekapcsolódni.
A témával kapcsolatos véleményemet itt olvashat(tad)-od:
http://file1.npage.de/001876/61/html/alf55.html
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@Vaszilov (67858):
Így bizony, sőt, a másik nagy szerencse, hogy a legtöbb anyagon áthatolni képes elektromágneses jelek sem léteznek, mert akkor minden elektromos berendezés összezavarná a másikat, és nem lehetne hallgatni a magunknál hordott magnetofont, főleg villamoson.Milyen szerencse, hogy nem létezik a gondolatátvitel! Tudnillik akkor villamoson, buszon, emberek csoportosulásában nem lehetne gondolkodni. Egymás gondolatai úgy összezavarnák az agyakat, hogy tökéletes tohuvabohu állna elő
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (67868): Marhaságot írsz, mert az elektromos készülékek éppen azért vannak leárnyékolva (ha tudod mi az?!), hogy ne zavarják egymást!!
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@Vaszilov (67871): Leárnyékolva, mint a rádió, ugye?  Szuperpozícióról és frekvenciák szerinti szétválaszthatóságáról még nem hallottál. Na, csak erre akartam rávilágítani, amikor butaságot mondtál a gondolatolvasás lehetetlenségéről.
Szuperpozícióról és frekvenciák szerinti szétválaszthatóságáról még nem hallottál. Na, csak erre akartam rávilágítani, amikor butaságot mondtál a gondolatolvasás lehetetlenségéről.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (67872): A gondolatolvasás, helyesebben a telepátia lehetetlenségéről az előzőleg mellékelt linken megemlítettem néhány érvet!
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@Vaszilov (67873): A cikkedben arról mesélsz, hogy elektromágneses hullámok révén valószínűtlen a telepátia. Valóban. Egy kölcsönhatást kizártál az ismertek közül, az ismeretlenekből meg ugye még egyet se  .
.
Aztán arról mesélsz, hogy a gondolatok mindenkinél más-más neurális mintázatokhoz kötődnek, ezért 1:1-ben átvinni őket aligha lehet. Persze, na és? Beszélgetni is tudunk, a telepátia miért ne működhetne hasonlóan jó interfészen keresztül?
Félre ne érts, egy szóval sem mondtam, hogy lehetséges, csak annyit, hogy az ellenérveit távolról sem zárják ki.
Aztán arról mesélsz, hogy a gondolatok mindenkinél más-más neurális mintázatokhoz kötődnek, ezért 1:1-ben átvinni őket aligha lehet. Persze, na és? Beszélgetni is tudunk, a telepátia miért ne működhetne hasonlóan jó interfészen keresztül?
Félre ne érts, egy szóval sem mondtam, hogy lehetséges, csak annyit, hogy az ellenérveit távolról sem zárják ki.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (67872): Feltetelezed, hogy a kulonbozo emberek agya kulonbozo frekvanciakon kuldi a jelet, es a gondolatolvasok fejeben vannak hangolo kutyuk, amikkel az ember rahangol egy masik emberre es kiszuri az osszes tobbit.
aha
aha
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (67878): Ha nem tetelezel fel ilyet, akkor Vaszilov erve helytallo.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@Vaszilov (67863):
ennyi
Nagyon jo, logikus, ertheto.Elolvastam az utolsó oldalt, de nincs kedvem bekapcsolódni.
A témával kapcsolatos véleményemet itt olvashat(tad)-od:
http://file1.npage.de/001876/61/html/alf55.html
ennyi
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@ennyi (67879):
A régi lemez... Szerinted, ha valamit nem zárok ki, akkor az ellenkezőjét feltételezem. Tévedés!Ha nem tetelezel fel ilyet, akkor Vaszilov erve helytallo.
0 x
A tudományos parapszichológiáról (a blog kapcsán)
@mimindannyian (67886): Tehat a "Szuperpozícióról és frekvenciák szerinti szétválaszthatóságáról még nem hallottál." kijelentesed nem azt jelenti, hogy te feltetelezned, hogy ilyen alapon mukodik a telepatia. OK, de akkor minek irtad ezt ide?
Ha ezt nem tetelezed fel, akkor ugye nincs erved es Vaszilov megallapitasat fogadjuk el:
Micsoda hangzavar, ha egyszerre egyforma hangerovel hallod az osszes ember beszedet.
Nyilvan ezert nem mukodnek a kiserletek, mert a kiserleti alany nem tudja, kire hallgasson. Egy valaki a negy kep kozul valamelyikre gondol, es kozben tobb milliard ember mind valami masra es kulonbozo dolgokra gondol.
Igy ertheto az eredmeny, hogy csak ritkan szuletik helyes valasz. Az lenne a meglepo es megmagyarazhatatlan, ha gyakarabban lehhe helyes valasz, ha figyelembe vesszuk, hogy a tobbi ember mind masra gondol.
Ha ezt nem tetelezed fel, akkor ugye nincs erved es Vaszilov megallapitasat fogadjuk el:
Mi tobb ezt kiterjesztjuk azzal, hogy agondolatatvitel a tavolsagtol fuggetlen, igy nem is kell hozza csoportosulas. Elegendo az, hogy tobb ember letezzen, barhol. Osszezavarjak egymas adasat.Tudnillik akkor villamoson, buszon, emberek csoportosulásában nem lehetne gondolkodni. Egymás gondolatai úgy összezavarnák az agyakat, hogy tökéletes tohuvabohu állna elő
Micsoda hangzavar, ha egyszerre egyforma hangerovel hallod az osszes ember beszedet.
Nyilvan ezert nem mukodnek a kiserletek, mert a kiserleti alany nem tudja, kire hallgasson. Egy valaki a negy kep kozul valamelyikre gondol, es kozben tobb milliard ember mind valami masra es kulonbozo dolgokra gondol.
Igy ertheto az eredmeny, hogy csak ritkan szuletik helyes valasz. Az lenne a meglepo es megmagyarazhatatlan, ha gyakarabban lehhe helyes valasz, ha figyelembe vesszuk, hogy a tobbi ember mind masra gondol.
0 x
- mimindannyian
- *

- Hozzászólások: 7918
- Csatlakozott: 2011.04.23. 16:20
- Tartózkodási hely: Szoboszló
A tudományos parapszichológiáról (a blog kapcsán)
@ennyi (67890):
Azért, hogy rávilágítsak, az ellenérve hibás. Ebből nem az következik, hogy van telepátia, csak az, hogy az ő indoklása nem elégséges, hogy annak lehetőségét kizárjuk.Tehat a "Szuperpozícióról és frekvenciák szerinti szétválaszthatóságáról még nem hallottál." kijelentesed nem azt jelenti, hogy te feltetelezned, hogy ilyen alapon mukodik a telepatia. OK, de akkor minek irtad ezt ide?
Nem, továbbra sem fogadom el. Gondolj csak a hanghullámokra. Az ő gondolatmenete szerint beszélgetni sem lehetne tömegben, hiszen egymás hangja úgy összezavarná a füleket.Ha ezt nem tetelezed fel, akkor ugye nincs erved es Vaszilov megallapitasat fogadjuk el:Tudnillik akkor villamoson, buszon, emberek csoportosulásában nem lehetne gondolkodni. Egymás gondolatai úgy összezavarnák az agyakat, hogy tökéletes tohuvabohu állna elő
A távolságfüggetlenségből nem következik, hogy mindenhol ugyanúgy hallasz mindenkit. Egy zárt fém csőben, melyben tegyük fel, hogy útjuk során semmit sem csillapodnának a rádiójelek, csak ide-oda verődnének, mint fény az üvegszálban, talán nem lehetne rádiózni?Mi tobb ezt kiterjesztjuk azzal, hogy agondolatatvitel a tavolsagtol fuggetlen, igy nem is kell hozza csoportosulas. Elegendo az, hogy tobb ember letezzen, barhol. Osszezavarjak egymas adasat.
Micsoda hangzavar, ha egyszerre egyforma hangerovel hallod az osszes ember beszedet.
Ez az érv egy feltételezett mechanizmus esetén állja meg a helyét, viszont mivel pont a mechanizmus kérdéses, nem sokat nyom a latban.Nyilvan ezert nem mukodnek a kiserletek, mert a kiserleti alany nem tudja, kire hallgasson. Egy valaki a negy kep kozul valamelyikre gondol, es kozben tobb milliard ember mind valami masra es kulonbozo dolgokra gondol.
Igy ertheto az eredmeny, hogy csak ritkan szuletik helyes valasz. Az lenne a meglepo es megmagyarazhatatlan, ha gyakarabban lehhe helyes valasz, ha figyelembe vesszuk, hogy a tobbi ember mind masra gondol.
0 x