Skalármezős infláció (kozmológia)

[szabiku]

Találtam két linket, ahol az Univerzum (korai) inflációs történetének matematikai modellje van tárgyalva.

http://astro.u-szeged.hu/oktatas/asztro ... l/all.html

Ezen belül: http://astro.u-szeged.hu/oktatas/asztro ... de165.html


Valamint: https://ned.ipac.caltech.edu/level5/Wat ... tents.html

És ezen belül: https://ned.ipac.caltech.edu/level5/Wat ... on5_3.html

Az infláció feltétele a gyorsuló tágulás, amely a Raychaudhuri-egyenlet értelmében .

Ez a feltétel szerintem ellentmondásban van a relativitáselmélettel.

[Rigel]

Az infláció feltétele a gyorsuló tágulás, amely a Raychaudhuri-egyenlet értelmében .

Ez a feltétel szerintem ellentmondásban van a relativitáselmélettel.

Az a te bajod.

Nincs ellentmondásban.
A Raychaudhuri-egyenlet (más forrásokban Friedmann gyorsulási egyenlet)

egyenesen levezethető a Friedmann-egyenletből, ami pedig az áltrel Einstein-féle téregyenleteinek egyik egzakt megoldása. Egyáltalán nincs ellentmondásban a relativitáselmélettel, mert eleve abból származik.

Az más kérdés, hogy az energiasűrűség és a nyomás helyére milyen értékeket helyettesíthetünk be. Normál anyagféleségeknél mindkettő pozitív, így a (ρ + 3p) is pozitív lesz. De ha véletlenül valaminek negatív a nyomása (pozitív energiasűrűség mellett, azaz "létező" dolog), akkor nagyon könnyen előfordulhat, hogy a (ρ + 3p) negatívvá válik, és akkor a fenti képletben szereplő mínuszt pluszba fordítja, ami pedig a skálaparaméter gyorsuló növekedését jelenti. (Idő szerinti második derivált!)
A kvantummezőelméletek szerint pedig a pozitív vákuumenergiának negatív nyomása van.

[szabiku]

Az a te bajod.

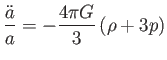
Nem csak az enyém, hanem az egész elképzelésé.

Nincs ellentmondásban.
A Raychaudhuri-egyenlet (más forrásokban Friedmann gyorsulási egyenlet) egyenesen levezethető a Friedmann-egyenletből, ami pedig az áltrel Einstein-féle téregyenleteinek egyik egzakt megoldása. Egyáltalán nincs ellentmondásban a relativitáselmélettel, mert eleve abból származik.

Ez hibás érvelés, ugyanis a Raychaudhuri-egyenlet az az, amit felírtál, de a követelés az egészen más. Ez egy körültekintés nélkül kitalált egyenlőtlenség a és értékeire, mert azt szeretné(n)k kierőszakolni (a megfigyelések alapján), hogy a tágulás ne lassuló, hanem gyorsuló legyen. Egyáltalán nem biztos, hogy ez a követelés összeegyeztethető a relativitáselmélettel. Az Einstein-egyenleteknek ehhez a követeléshez már semmi köze, és ezért valóban:

... más kérdés, hogy az energiasűrűség és a nyomás helyére milyen értékeket helyettesíthetünk be.

Na itt van a kutya elásva!

A relativitáselmélet nem ismeri a negatív nyomást.

Tettem kísérletet annak beleillesztésére ( viewtopic.php?f=8&t=898 viewtopic.php?t=898&start=27 ), de ez csupán az elmélet kis átverése, és nem más.

A relativitáselmélet valójában nem ismeri a negatív nyomást.

[Rigel]

A relativitáselmélet nem ismeri a negatív nyomást.

Csak te nem ismersz negatív nyomást.

A relativitáselmélet csak p nyomást ismer. Azt viszont nem köti meg, hogy p értéke mi.
A p helyére meg olyan értéket helyettesíthet be mindenki, amit a valóságban mér. Alan Guth például kvantummezőelméleti megfontolásokból negatív nyomást helyettesített be.

[szabiku]

Én úgy gondolom, hogy a nyomás az a klasszikus (nem kvantumos) leírású anyag mechanikája alapján értelmezett (izotróp) fizikai mennyiség. Ez csupán helyet kap a diagonális alakú energiaimpulzus-tenzor megfelelő komponensében, de az nem igaz, hogy az energiaimpulzus-tenzor ezen komponense teljes egészében meg általánosan az izotróp nyomást jelenti (és ez már a mechanika esetében is nyilvánvaló, ha pl. a nem izotróp esetre gondolunk..). Jó példa erre a kvantumelmélet beötvözése az általános relativitáselméletbe az Univerzum (korai) inflációs történetének matematikai modelljében. A kvantumtérelméleti skalármező NEM olyan, mint egy relativisztikus ideális klasszikus szerkezetű folyadék, és egyáltalán NEM is úgy viselkedik. Nem szerencsés ebben így a jelölést használni, és egyáltalán nem szabadna itt azt nyomásnak nevezni.

[con]

Ha szabiku nem akar nyomásról beszélni és p betűt használni, nyugodtan megteheti, hiszen az energiaimpulzus-tenzor térXtér-szerű 3X3 komponensében a három impulzuskomponens áramsűrűségeinek 3-3 komponense van. Ezek közül a Tˇxx-ben Tˇyy-ban és Tˇzz-ben az impulzusáram-vektor (vagyis az erő) x, y, z komponense merőleges arra a felületelemre, amin átadódik. Ezeket az erősűrűségeket a mechanikában hagyományosan nyomásnak nevezik. Míg a vegyes indexű tenzorelemeket, nyírásnak, mert bennük az erőkomponens párhuzamos az átadófelülettel.

Ám ez csak szóhasználati kérdés. Szabiku viszont valamiképp meg akar szabadulni a Tˇii negatív értékeitől. Ezért állítja, hogy azok ellentétben állnának a relativitáselmélettel. És efféle szómágiával akarja diszkreditálni:

Ez csupán helyet kap a diagonális alakú energiaimpulzus-tenzor megfelelő komponensében, de az nem igaz, hogy az energiaimpulzus-tenzor ezen komponense teljes egészében meg általánosan az izotróp nyomást jelenti

A kevésbé tájékozott olvasók számára írom, hogy erről szó sincs. Jól is néznénk ki, ha a relativitáselmélet nem tudna mit kezdeni a negatív nyomással, vagyis a húzófeszültséggel.

[szabiku]

Egyáltalán nem csak szóhasználati kérdés, hanem nagyon is lényeges értelmezési és matematikai kérdés.

Szabiku viszont valamiképp meg akar szabadulni a Tˇii negatív értékeitől.

Normál anyag esetére igen. És ezt az entalpiára hivatkozva egyszerűen be is láttam:

Ha az energiaimpulzus-tenzorba egyszerűen negatív értékű (izotróp) nyomást veszünk, akkor az lesz a gond, hogy az entalpia ugyanakkora nyugalmi energiasűrűség mellett nagyobb negatív nyomás esetén kisebb lesz, ami nem lehet, hiszen a nagyobb negatív nyomás eléréséhez pozitív energiát kell befektetnünk széthúzás közben.

Ezért állítja, hogy azok ellentétben állnának a relativitáselmélettel.

Igen, ezért.

Jól is néznénk ki, ha a relativitáselmélet nem tudna mit kezdeni a negatív nyomással, vagyis a húzófeszültséggel.

Akkor áruld el, ebben hol a hiba:

Ha az energiaimpulzus-tenzorba egyszerűen negatív értékű (izotróp) nyomást veszünk, akkor az lesz a gond, hogy az entalpia ugyanakkora nyugalmi energiasűrűség mellett nagyobb negatív nyomás esetén kisebb lesz, ami nem lehet, hiszen a nagyobb negatív nyomás eléréséhez pozitív energiát kell befektetnünk széthúzás közben.

Én megmondom, hogy nálad hol a probléma:

... az energiaimpulzus-tenzor térXtér-szerű 3X3 komponensében a három impulzuskomponens áramsűrűségeinek 3-3 komponense van. Ezek közül a Tˇxx-ben Tˇyy-ban és Tˇzz-ben az impulzusáram-vektor (vagyis az erő) x, y, z komponense merőleges arra a felületelemre, amin átadódik. Ezeket az erősűrűségeket a mechanikában hagyományosan nyomásnak nevezik. Míg a vegyes indexű tenzorelemeket, nyírásnak, mert bennük az erőkomponens párhuzamos az átadófelülettel.

A hagyomány a rózsaszín köd. Az aláhúzás (egy speciális esetet leszámítva, tehát általában) mind HIBÁS vonatkozás.

Tájékoztatlak, hogy pl. a vákuumbeli elektromágneses mező pontjaiban nem értelmezünk se nyomást, se nyírófeszültségeket, sem mechanikai erőt vagy mechanikai erősűrűséget. Ezek csupán közvetítődnek. (És még csak nem is kvantumtérelméleti példát hoztam fel, hanem egy klasszikus elektromágneses mezőt.)

A másik hibád pedig az, hogy az említett hagyományos megfeleltetés is csak akkor áll, ha az anyag nyugalmi rendszerében vagyunk, különben (tehát általában) NEM. Házi feladat ennek belátása.

[srudolf]

Szabiku, megint elszálltál.
Nézd meg ezt az ábrát.
Az piros bázisvektorokhéz képest, bármelyik szigma mechanikai feszültség lehet pozítív vagy negatív- a külső hatás függvényében. Azokat a szigmákat nyomásnak is lehet nevezni, hiszen fizikai értemezése teljesen azonos a mechainikai feszültséggel.
Az energia-impuzus tenzor csak annyiban külömbözik, hogy megjelennek az energia jellegű hatások is, az időszerű komponensekkel.

Még kéne egy bázisvektor és már 4 dimenzióba lennénk.

[con]

Szabikut hallgatva már csak az nem fér a fejembe, hogy ez a zseniális ember miért egy ilyen laikus fórumon vergődik, ahelyett hogy felvilágosítaná a világ fizikusait a tévedéseikről, és kivezetné őket ebből a zsákutcából. Hogy rájöjjenek végre, csak egy rossz álom volt, amit pedig az elmúlt 35 év legnagyobb felfedezésének képzeltek. Az inflációs kozmológia.

[szabiku]

Con, az inflációt nem cáfoltam, csak azt, hogy benne nyomásnak nevezzük a -vel jelölt mennyiséget (és nem csak az esetleges negatív értéke miatt, hanem a származása miatt).

Szabiku, megint elszálltál.

Nem, csak próbálom rendbe rakni a dolgokat.

Nézd meg ezt az ábrát.
Az piros bázisvektorokhoz képest, bármelyik szigma mechanikai feszültség lehet pozitív vagy negatív a külső hatás függvényében. Azokat a szigmákat nyomásnak is lehet nevezni, hiszen fizikai értelmezése teljesen azonos a mechanikai feszültséggel.

Az aláhúzás ellentétben áll az entalpiával, és ez a relativitáselméletben, ahol bizonyos hármasskalár mennyiségek négyes mennyiségekké egészítenek ki magasabb rendű hármas mennyiségeket, gondot okoz:
Ha az energiaimpulzus-tenzorba egyszerűen negatív értékű (izotróp) nyomást veszünk, akkor az lesz a gond, hogy az entalpia ugyanakkora nyugalmi energiasűrűség mellett nagyobb negatív nyomás esetén kisebb lesz, ami nem lehet, hiszen a nagyobb negatív nyomás eléréséhez pozitív energiát kell befektetnünk széthúzás közben.

Az energia-impulzus tenzor csak annyiban különbözik, hogy megjelennek az energia jellegű hatások is, az időszerű komponensekkel.
Még kéne egy bázisvektor és már 4 dimenzióba lennénk.

aláhúzás: Hát éppen hogy NEM! (A házi feladat: egyes..)

Az ábrán szereplő 3x3-as szigma mennyiség NEM része a 4x4-es energiaimpulzus-tenzornak. Házi feladat (ismét) ennek belátása.

[con]

De része, ha nincs anyagáramlás.

[szabiku]

Na igen, "ha nincs anyagáramlás"... (Próbálod kivágni magad )
Vagyis inkább úgy fogalmaznék, hogy a hagyományos (és elektromágneses tértől mentes) anyag nyugalmi rendszerében éppen mind megegyeznek az értékei a szimmetrikus energiaimpulzus-tenzor térszerű komponenseinek értékeivel. És hogy csak akkor, annak egyik oka az, hogy a térbeli felületelem normális vektora egyformán transzformálódik a mechanikai hármaserővel. Nyírófeszültségeknél viszont ezek éppen merőlegesek egymásra, és ezért nem egyformán transzformálódnak másik inerciarendszerbe a és komponensek, mert ezek a következő szerint erő/felület jellegűek: . Egy szimmetrikus tenzornál, mint pl. az energiaimpulzus-tenzor, pedig nyilván egyformán transzformálódnak a és komponensek, hiszen azonosak. A nem egyezőség egy másik oka pedig az, hogy a komponensekbe beletranszformálódik a nyugalmi rendszerbeli komponens is. Egy harmadik ok pedig az, hogy egy kvantumtérelméleti skalármezőre nem értelmes a mennyiség (nyilván a nyomással együtt), hasonlóan ahogy pl. a klasszikus elektromágneses mezőre sem.
Megtévesztő, hogy hagyományból feszültségeknek nevezzük a térszerű komponenseket is, ahogy a hagyományos anyagra értelmezett mennyiség komponenseit, pedig csak az utóbbiak jelentenek mechanikai feszültségeket.

[con]

Az elektromágneses sugárzás nyomása egy elemi jelenség, a skalármezőké szintúgy közismert. Ez az egész szöveg újra egy tipikus szabiku halandzsa. Úgy torlasztja egymásra a különböző félreértéseket és a blöfföket, hogy az embernek semmi kedve szétszálazni. Az érdeklődőknek csak azt tudom mondani, ne is próbálkozzanak a megértésével. Jobban járnak, ha Hraskó Péter Relativitáselmélet c. könyvét tanulmányozzák. Abból igen világosan megtanulhatják mi is az energiaimpulzus-tenzor.

[szabiku]

Össze-vissza keversz...
Mit értesz az elektromágneses sugárzás nyomása alatt??

Azt, amit a fénysugár közvetít egy hagyományos anyagfelületre? Ez kapufa..
Vagy pedig a kozmológiában szeretettel használt (izotróp) "fénygáz" szerű idealizált lehetetlen határesetet? Ez is kapufa, mert az egy elméletileg már ellentmondásos határeset.. (Ami egyébként matematikailag egy összekötőpont, és ezért hasznos bizonyos elméleti számításokban, levezetésekben..)

Nincs olyan elemi jelenség, hogy az elektromágneses sugárzásBAN nyomás (azaz mechanikai feszültség) van.

[con]

Mit értesz az elektrosztatikus mező egy pontban érvényes térerőssége alatt?
Az odahelyezett egységnyi próbatöltésre ható erőt.
Így definiálják a tér minden pontjában.
Akkor is, ha nincsenek a tér minden pontjában próbatöltések.
Úgy mérik, hogy ténylegesen odatesznek egy próbatöltést
Ugyanígy van értelmezve a többi mező térerőssége is.
És ugyanilyen módon definiálják az elektromágneses sugárzás nyomását a tér minden pontjára, az odaképzelt elnyelő rendszerre (pl. atomra) ható erő alapján. Akkor is, ha történetesen nincs is ott semmi, és nem nyelődik el ott a sugárzás.
Úgy mérik, hogy ténylegesen odatesznek egy nyelőt.

A fizika nem bölcsészkedés, hogy efféle ködfüggönyökbe burkold:
"lehetetlen határeset",
"elméletileg már ellentmondásos határeset",
"ami egyébként matematikailag egy összekötőpont",
"és ezért hasznos".
De nem is foci, amiben értelmes kijelentés a "kapufa".
Ezekkel csak te maszatolsz.

[szabiku]

Mekkora nyomás uralkodik az elektromágneses síkhullámban?? (vákuumban)

[con]

Ezt igazán minden szakkönyvben megtalálhatnád.
De látom te inkább ezekbe az éretlen zöld vigyorkákba vagy beleszeretve. Kinőhetnél már a kamaszkorból!
Lásd:
Hogy ne legyen sok felesleges konstans, a Gauss mértékegység rendszerben írom.

Amikor csak elektromágneses mező van jelen:
Az energiasűrűség:

Az energiaáramlás sűrűsége, vagyis a Poynting vektor:

A sugárzás impulzusa:

És a Maxwell-féle feszültségtenzor főátlójában lévő nyomás típusú tagok (sugárnyomás):

Végül a többiek:

Máshol találkozhatsz ettől némileg eltérő formulákkal, de a ismeretében nem jelent gondot összevetni ezekkel.

A fentiek a közönséges (tömeges) anyagtól mentes elektromágneses térre igazak. Ha töltött vagy töltetlen részecskék is jelen vannak, akkor hozzá kell adni az ő energia-impulzus tenzorukat is. Így megy ez mindaddig, míg a részecskék egymással való kölcsönhatásai elhanyagolhatók, és a kialakuló eredő gravitációs tér is annyira gyenge, hogy az Einstein egyenlet nonlinearitása nem rontja el az additivitást.

[con]

Az elektromágneses mező fontos esete a forrásaitól (töltések és áramok) függetlenné vált szabad elektromágneses hullám. Ha az ilyen tisztán sugárzási tér egy síkhullám módusát nézzük, a hozzzá tartozó és vektorok mindig merőlegesek egymásra, és a hullám impulzusvektora, továbbá energiaáram vektora merőleges lesz az és által kifeszített síkra. Ebben az esetben sokat egyszűsödik a tenzor, így ha az mondjuk az x tengely irányába, a pedig az y irányába mutat, akkor csak a négy sarokban lévő komponensek különböznek nullától.
A bal felsőben az energia:
,
jobbra felül az energiaáram:
,
balra lenn ennek szimmetriapárja, az impulzus:
,
végül jobbra lenn a nyomás:
.
Látható, hogy az ilyen párhuzamos fénynyaláb sugárnyomása épp akkora, mint az energiasűrűsége.

Vegyünk ezután ugyanilyen energiájú, de x és y irányú nyalábokat, ezekre hasonló úton kapjuk, hogy


Ha a három egymásra merőleges nyalábot egyszerre tesszük be a tenzorba (tudva, hogy a vákuumban egymást keresztező fénynyalábok között nem keletkezik kölcsönhatás), akkor az energiáik a képletből következő módon összeadódnak, miközben nyomásaik a főátlón külön, külön tenzorkomponensbe kerülnek. Tehát az eredő rendszer energiája: , így aztán:


Nézzünk ezután egy hullámteret (diffúz szabad fotongázt), ami energiától független egyenletes iránybeli eloszlással tartalmaz mindenféle síkhullámokat. Képzeletben bontsuk fel ezeket a koordináták irányába eső komponensekre. Nyilvánvaló, hogy az x, y és z irányú összetevők átlagos energiái azonosak lesznek, így középértékben erre a diffúz sugárzásra is igaz lesz a fenti összefüggés, amit röviden az állapotegyenletként írnak.

[szabiku]

Én értékelem a szorgalmad, de sajnos nem jók a részletesen felvázolt elképzeléseid.
A kiindulás az O.K., én is látom a Landau II könyv 113. oldalán, és a Novobátzky könyv 59., valamint 81. oldalán.

A gond az, hogy te végig az energiaimpulzus-tenzor térszerű 3x3-as elemeit tekinted a mechanikai feszültségeknek bármelyik inerciarendszerben. Ez nem stimmel, és ezt fentebb le is írtam. A Landau könyv ebben megtévesztő, mert (32,15)-ben szigma jelölést alkalmaz, holott ezek a komponensek a relativitáselméletben NEM a hagyományos mechanikai feszültségeket jelentik (csak legfeljebb a nyugalmi rendszerben jelenthetik azokat..), hanem a lokális tér "feszültségeit", és csak rajtamaradt (hagyományból és talán a megmaradt impulzussűrűség-áramok jelentése miatt) az a roppant megtévesztő elnevezés, hogy "feszültség". Mechanikai feszülést ez utóbbi már NEM jelent. Novobátzky ezt ki is hangsúlyozza a könyve 104. oldala alján. Ő -val jelöli a relativisztikus mechanikai feszültségeket (203), és nyilván csak 3x3=9 térszerű komponens van értelmezve. De ami az energiaimpulzus-tenzorba ez alapján beépül, az nem az általában nem szimmetrikus (amit ugye a nemrelativisztikus korábbi mechanikában jelöl), hanem a szimmetrikus (207) !! Ezt egyszerűen te nem akarod megérteni, pedig nem nehéz belátni.

A Landau II könyv a 118. oldalon ezt írja:

"A test felületelemén átfolyó impulzusáram valójában az erre az elemre ható erő. Ezért a felületelemre ható erő -adik komponense. Tekintsük most azt a vonatkoztatási rendszert, amelyben a test adott térfogateleme nyugalomban van."

A könyv alapján, hogy a mennyiséget azonosnak veszi -val, sajnos ez HIBÁS kijelentés.
Így lenne jó (pl. a Novobátzky könyv 102-103. oldalai alapján):
Tekintsük azt a vonatkoztatási rendszert, amelyben a test adott térfogateleme nyugalomban van. Ekkor a test felületelemén átfolyó impulzusáram valójában az erre az elemre ható erő. Ezért ekkor(!!) a (nyugvó) felületelemre ható erő -adik komponense. Más vonatkoztatási rendszerben az erő (hármaserő) komponensei egy mennyiséggel írható fel összegező formában, ami a Novobátzky könyvben szereplő (203) képletek alapján transzformálódik.

Ha ennek a hibának a belátása és megértése után visszatekintünk a (32,15)-ben alkalmazott szigma jelölésekre, akkor látható, hogy semmi értelme a komponenseket -val jelölni, sőt hibás is, mert az másik mennyiség, másképpen is transzformálódik, és akkor jó lehetne a 118. oldalról beidézett rész.

A mechanika szerint a rugalmas feszültségek jelentik a mechanikai feszültségeket, és ezek jelentenek nyomást meg nyírást.
A tér "feszültségei", tehát az energiaimpulzus-tenzor (már fentebb is ehhez a felsőindexes alakját kellett volna venni...) térszerű 3x3-as komponensei közvetlenül NEM jelentenek nyomást és nyírást, és nemközvetlenül is csak akkor, ha hagyományos és ugye nyugalmi rendszerrel is rendelkező anyag van ott, mert ekkor létezik csak a kapcsolódó (direkt nem szigmával jelölöm most..) mechanikai feszültségek (benne a nyomással).

És a Maxwell-féle feszültségtenzor főátlójában lévő nyomás típusú tagok (sugárnyomás)

A Maxwell-féle feszültségtenzor nyilván az úgynevezett "térfeszültségek". Az aláhúzott "típus" szó nyilván fosztani akarja az előtte álló "nyomás" szót a tényleges mechanikai jelentésétől. Igen, az általam elmondottak alapján ez kell is. DE ez NEM jelenti a sugárnyomást. A "sugárnyomás" fogalom az tényleges mechanikai nyomást jelent, ami nyilván ütközés szerű kölcsönhatás által jön csak létre. (Kell hozzá, hogy ott legyen valami, amivel ütközik a fénysugár, és ténylegesen, nem csak odaképzelve...) A sugárnyomás, mint nyomás invariáns skalár. Amit te annak nevezel, az nem invariáns:

Látható, hogy az ilyen párhuzamos fénynyaláb sugárnyomása épp akkora, mint az energiasűrűsége.

Ebből is látható a tévedésed.
És hasonlóan ez sem igaz:

... definiálják az elektromágneses sugárzás nyomását a tér minden pontjára, az odaképzelt elnyelő rendszerre (pl. atomra) ható erő alapján. Akkor is, ha történetesen nincs is ott semmi, és nem nyelődik el ott a sugárzás.

Az igazamat nem cáfolja a fény (érdekes és csodálkoztató) termodinamikája, mert abban, ahogy azt fentebb írtam, klasszikus formában kétséges fény van. (A fény kvantumossága, és a kvantumelmélet valószínűségi jellege matematikailag az átlagolást közelfekvővé teszi, és így összetalálkozik a már lehetetlen extrém relativisztikus határeset az izotróp formájú fényszerűséggel.)

Vegyünk ezután ugyanilyen energiájú, de x és y irányú nyalábokat, ezekre hasonló úton kapjuk, hogy


Ha a három egymásra merőleges nyalábot egyszerre tesszük be a tenzorba (tudva, hogy a vákuumban egymást keresztező fénynyalábok között nem keletkezik kölcsönhatás), akkor az energiáik a képletből következő módon összeadódnak, miközben nyomásaik a főátlón külön, külön tenzorkomponensbe kerülnek. Tehát az eredő rendszer energiája: , így aztán:

Ez hatalmas nagy tévedés, egyszerűen HIBÁS!!
Így te az izotróp fotont vagy sugárzást akarod "előállítani", ami elméletileg sem létezik.
Az elektromágneses térerősségek additívak, és nem a komponenseik szorzatai (!!), amiből az elektromágneses mező energiaimpulzus-tenzora áll. Ezzel közvetlen kapcsolatban áll az, hogy a fény vagy foton energiaimpulzus vektora sem additív. A zárójeles hivatkozásod, hogy klasszikusan nem hatnak kölcsön a fénynyalábok, ezt nem változtatja meg. (A matematikai hibád nagyon alapvető..)

Nézzünk ezután egy hullámteret (diffúz szabad fotongázt), ami energiától független egyenletes iránybeli eloszlással tartalmaz mindenféle síkhullámokat. Képzeletben bontsuk fel ezeket a koordináták irányába eső komponensekre. Nyilvánvaló, hogy az x, y és z irányú összetevők átlagos energiái azonosak lesznek, így középértékben erre a diffúz sugárzásra is igaz lesz a fenti összefüggés, amit röviden az állapotegyenletként írnak.

Az elképzelés ilyen leírása már kezd jó lenni, de a mögötte lévő részleteket tekintve jobban át kell azt gondolni. Nem csak a három x, y, és z irányú összetevőkről van szó, hanem minden irányú hullámösszetevő különálló összetevő, és ezért külön-külön számítódnak fel. (Ez is alapvető matematika a hullámok világában..) Az elektromágneses tér kvantálásánál sem csak a három x, y, és z irányú bázisok vannak, hanem minden más-más irányultságú hullám más-más bázishalmazba tartozik.

[con]

Nem gyanús neked szabiku, hogy mindenki szembe megy veled az autópályán? Landautól kezdve, szinte az egész mértékadó szakirodalom, amiben szó szerint úgy állnak a dolgok, ahogy leírtam.
Én többet nem akarok ilyesféle lila ködös dumákat olvasni:

Az igazamat nem cáfolja a fény (érdekes és csodálkoztató) termodinamikája, mert abban, ahogy azt fentebb írtam, klasszikus formában kétséges fény van. (A fény kvantumossága, és a kvantumelmélet valószínűségi jellege matematikailag az átlagolást közelfekvővé teszi, és így összetalálkozik a már lehetetlen extrém relativisztikus határeset az izotróp formájú fényszerűséggel.)

De a többi szöveged és matematikai umbuldád is valami hihetetlenül nyakatekert, fontoskodó, vágy-vezérelt és önámító. Ha a valódi fizikai irodalom ilyesmikkel operálna, eszembe se jutna egyet is elolvasni, ugyanúgy földhöz vágtam volna mind, mint a marxista filozófiát meg a politikai gazdaságtant.
Végleg elbúcsúztunk.

[szabiku]

Lefeküdtél?

... szakirodalom, amiben szó szerint úgy állnak a dolgok, ahogy leírtam.

A nyomás az invariáns skalár mennyiség, nálad meg nem.. Ennyi. Kereszt.
De ezért nem kell vergődnöd. Tanulságos volt ez a példa, és éppen jól rá is világított a kérdéses dolog velejére, szembeállítva a Landau II könyvet a Novobátzky könyvvel.

Én többet nem akarok ilyesféle lila ködös dumákat olvasni: ...

Bocs, hogy nem fejtettem ki bővebben. Hosszú lett volna. Talán majd máskor. Addig a többi hasznos információm alapján láss tisztábban, érts mélyebben, és tanuld meg, hogy sosem szabad bigott szellemmel fizikázni. A könyveket (főleg ilyen magas fokon) mindig fenntartásokkal kell tanulmányozni! Hibázni emberi dolog, és még a nagyokkal is megesik, ezért nem szentírás egyik fizikakönyv sem minden pontján.

[mimindannyian]

Még mindig nem kaptunk választ arra a sokszor felvetett kérdésre, hogy miért nem szakmai folyóiratokba küldi be szabiku a fizikus társadalom számára igen fontos észrevételeit.

[szabiku]

Ez valóban jó lenne, és már ki is néztem pl. a Magyar fizikai folyóiratot (ha még létezik). Picit terjedelmes munkáim vannak, és nincs értelme összepréselni csupán pár oldalba, mert csak a kellő terjedelemében és részletességében érthető meg. Úgyhogy olyan kiadványt érdemes erre használni amiben erre van elég kapacitás. (Megjegyzem a leszólások miatt, hogy semmi nagy újdonságot nem alkottam, csupán egy-két fontos és neves szakirodalomban fellelhető eltévelyedést világítottam meg, és javítottam.)
Csinálok egy honlapot (ami már félig kész), és abban megtalálhatók lesznek azok, amiket írtam, nagyon apró módosításokkal.
Még agyalok egy fontos dolgon: a hamisságán, vagyis a feltártak után annak Lagrange-sűrűséges hatásvariációs matematikai pontos megvilágításán (mert az egyrészt kell a görbült téridős gravitáció elméletében a megmaradásokkal kapcsolatban egy korábbi munkám némi pontosításához...), és közben vizsgálom a kvantumelmélet viszonyulását.

[mimindannyian]

Nagyszerű. Tedd fel egy honlapra a munkád, amilyen részletesen csak akarod, de hozd le hivatalos folyóiratban összefoglalóan. Nyilván többről van szó, mint elütések korrekciója, tehát tömören ki lehet gyűjteni az állításaid, s aki elsőre nem érti meg, majd elolvassa a részleteket. Hadd legyen rálátása azoknak, akiknek ez igazán fontos, akik munkáját előrébb lendíti! Tedd lehetővé a fizika megújhodását!

[szabiku]

Igen, ez a kombináció lesz majd szerintem is a legjobb. Köszönöm a biztatást.
Az elmúlt két napban sikerült is előrehaladnom az említett dolgok belátásában.
Nagyon fontos módszer a hatásvariációs eljárás, úgyhogy örülök, hogy végre sikerült átgondolnom a sarkalatos pontjait.

[szabiku]

Visszatérve még erre a "Van-e a fényben nyomás?" dologra, amiből api.con példáján keresztül látható, hogy mekkora félreértések keverednek, nézzük meg Hraskó Péter jegyzetének ( http://peter.hrasko.com/files/full5.pdf ) 99. és 100. oldalát, ahol ő szintén kihangsúlyozza azt, hogy az EM-mezőBEN van a nyomás:

... Ez az a lépés, ahol kihasználjuk, hogy az elektromágneses mezőnek van nyomása, mert különben az energia-impulzus tenzorának kontrakciója nem lehetne nulla.

Ez ugye hibás kijelentés és érvelés. A tévhit egyrészt onnan ered, hogy az energiaimpulzus-tenzorral foglalkozó 25. pont (61-64. oldalak) abban a tekintetben is hibásak (csak úgy, mint a Landau könyv), hogy ott a szerző érezhetően és szinte konkrétan abban a tévhitben van, hogy az energiaimpulzus-tenzor térszerű 3x3-as komponensei bármelyik vonatkoztatási rendszerben a rugalmas mechanikai feszültségeket jelentik, ha leszámítjuk a kinetikai részt. Ebben a tekintetben a Novobátzky könyv a jó (102-104. oldal). Másrészt pedig a helyzet az, hogy a (3p,p,p,p) diagonális alakú energiaimpulzus-tenzor átlagolással kétféleképpen kapható meg. Az egyik módon úgy, hogy minden frekvencián, pillanatnyi fázison és irányon EM hullámokat átlagolunk. (* *) Ezzel viszont az lesz a probléma, hogy így teljesen eltűnnek a hullámok, mert a térerősségek kiejtik egymást, viszont az egyes hullámösszetevő komponensek komponenseinek négyzete az megmarad, és azok adják a diagonális tagokat. A másik módon pedig úgy, hogy egymással nem kölcsönható, tehát nem ütköző, de mégis minden irányban mozgó kinetikus pontszerű részecskéket átlagolunk, és a sebességükkel a fénysebességhez tartunk, miközben a tömegükkel a nullához. ( http://www.tankonyvtar.hu/hu/tartalom/t ... x1-53006r5 ) Ez is ellentmondásos a javából, de mivel csodálatos módon a statisztikus kvantumelmélet (és annak egyéb jellege) a fény esetében ezt a helyzetet matematikailag (és így szinte fizikailag is) jobban lehetségessé teszi (ezt is nyugodtan meg lehet tőlem kérdezni, hogy miért..), ezért ez nem elvetendő, hanem egy hasznos kapcsolati eset. Másrészt mivel ugyan azt az említett energiaimpulzus-tenzort kapjuk mindkét kiindulásból csodálatos módon, az ilyen fény (kvantumos EM tér) tehát a fizika szerint az extrém relativisztikus határesetű (p=ε/3) ideális kinetikus gázhoz teljesen hasonlóan kell, hogy viselkedjen. És ez csodálatos módon így is van. DE ebben az esetben sem fogadható el a következő aláhúzott kijelentés:

... a szóban forgó térfogatban az energia csökken, a sugárzási tér - amelynek az energiasűrűség mellett nyomása is van - munkát végez a téridőn.

Még egyszer kihangsúlyozom, hogy ez egyáltalán nem jelent olyat, hogy az elektromágneses hullám(ok)BAN nyomás van, hiába hangzik vagy látszik úgy. A folytonos elosztottság minden ponthoz szétválaszthatatlanul rendel a fény mellett klasszikus kinetikus anyagot is, és csupán ez értelmez nyomást minden pontban. Egyszerűen látható, hogy ha csak a fény volna, akkor eltűnne az energiaimpulzus-tenzor átlós összege, és a skalár görbületet egyedül a kozmológiai állandó határozná meg. A (41.6) jobb oldala ekkor nulla. Semmilyen munkát nem végezne semmilyen nyomás a téridőn. Láthatóan minden részében teljesen hamis (41.6) után az a kijelentés, hogy:

Ez az a lépés, ahol kihasználjuk, hogy az elektromágneses mezőnek van nyomása, ...

A klasszikus kinetikus anyag nélkül összeomlik az egész számítás, és az eggyel előbb idézett következtetés egyenlete is eltűnik, ezzel egyértelműen mutatva annak hamisságát. (Ha pedig egy hatalmas, és tükröző falakkal rendelkező dugattyús térben lenne ez a tiszta fény, akkor is csak a falaknál lehetne értelmezni a nyomást, és nem pedig a fényben...)

(* *) A jelzett helyen kell észrevenni, hogy (az egyébként bozon esetű) hullámok tekintetében ez az átlagolás felvet egy újabb problémát, kérdést. Az egyes hullámösszetevők nem egy térbeli ponthoz tartoznak, hanem kiterjedésük miatt véges, vagy akár végtelen nagy tartományhoz. Tehát a kérdés az, hogy az egyes hullámösszetevőkhöz mekkora energia (vagy ezzel összhangban energiasűrűség) tartozik. Sőt inkább az, hogy az energia (vagy egy térbeli pontot tekintve az energiasűrűség) milyen eloszlást mutat a különböző frekvenciájú hullámösszetevőkre (ugye mivel a(z azonos) fermionok nem lehetnek azonos állapotban, ott ilyen probléma nem merül fel, ezért említettem előbb zárójelben a bozon esetűséget egy előretekintő megjegyzésként..). Ebből a problémából született a kvantumosság elmélete, melyhez ugye volt egy kísérleti megfigyelés, a hőmérsékleti sugárzás, amely ekkorra már (azt hiszem teljesen) világos volt, hogy elektromágneses sugárzás. A termodinamika pedig már kidolgozott elmélet volt a kinetikus gázelmélet alapján, sőt a kinetikusság fölé is nőtt az entrópiával, így bizonyos esetben a fényhullámok (vagy EM hullámok) energiaeloszlására is meghatározó, ami az éppen most fejtegetett kérdés. Ez persze megint nem azt jelenti, hogy az elektromágneses hullámBAN, vagy hullámokBAN mechanikai nyomás van, hanem csupán azt, hogy a fent tárgyalt átlagolásnál, ha speciálisan Planck-eloszlást veszünk, akkor az a termodinamikai egyensúly állapotát jelenti a sugárzási tér, és a sugárzást kibocsájtó és egyben elnyelő anyag között. Valamint ezzel egyéb, pl. az úgynevezett "ultraibolya katasztrófa" elnevezésű ellentmondás is elkerülődik. Így szépen összeérnek a fizika egyes területei, ami csodálatosan szépnek és elvártnak is mondható, de azért vigyázni kell, hogy bizonyos fizikai fogalmakat (mint pl. a mechanikai nyomás) az értelmüknek csak megfelelő helyen használjuk, hiszen az csak így következetes. A következetlen átemelések nyilván hibásak, és nagyon megtévesztőek, félrevezetőek tudnak lenni, valamint erősen gátolják a helyes felfogást, amit bizonyos esetekben csak eléggé szőrszálhasogató átgondolásokkal lehet tisztázni.

[szabiku]

Maradva még egy picit a mechanikai feszültségeket jelentő mennyiségnél (ami ugye csak a nyugalmi rendszerben esik egybe a komponensekkel, és melyeket Novobátzky a könyvében -val jelöl), vizsgáljuk meg a Novobátzky könyv 107-108 oldalainak erre vonatkozó állításait. Sajnos ezeken az oldalakon is súlyos hibák találhatók (akárcsak az utána következő 42. Az impulzusmomentum tétele című pontban, amit már kifejtettem egy másik topikban viewtopic.php?f=8&t=915&start=5 ).

A 103. oldalon (203)-ban látható, hogy nem szimmetrikus, csak a nyugalmi rendszerben, ezért nem is lehet része négyestenzornak, mert ugye akkor annak a nem nyugalmi rendszerben is szimmetrikusnak kellene lennie.

Nézzük akkor miről is van szó:

"Feleletet adunk még a fentebb felvetett kérdésre, hogyan kaphatók a rugalmas feszültségek a lokális feszültségekből. A mechanika szerint adja a térfogatra ható erő komponensét, mely a térfogatban foglalt impulzus idő szerinti differenciálhányadosával egyenlő:

.

Itt felhasználtuk (195)-öt. A jobb oldali tagban külön írjuk az szerinti differenciálhányadost, és tekintetbe vesszük, hogy .

(215) ."

Ez idáig tökéletesen jó, és mondhatni ezek a rugalmas kontinuumra vonatkozó relativisztikus dinamika "mozgásegyenletei". Azért csak mondhatni, és azért használtam idézőjelet, mert a tényleges mozgást ezek még nem adják meg, hiszen ahhoz az anyag állapotegyenlete is szükséges, aminek megfelelően az egyes térpontokban energiasűrűség jellegű invariáns nyugalmi mennyiségek alakulnak át, ahogyan azt említettem a már hivatkozott topikban viewtopic.php?f=8&t=915&start=6 . Szerencsére (és talán nem is véletlen) a könyvben itt éppen el van kerülve az "erő", és a négyes erősűrűség vektor jele, hiszen az tartalmazza (a komponenseiben) az állapotegyenlet(ek) szerinti energiaátalakulásoknak megfelelő komponenseket is, ami ugye a nyugalmi rendszerben az erősűrűség negyedik komponense. (Ugye ettől nem merőleges általában a négyeserő(sűrűség) a négyeselmozdulásra, és ez jelenti a négyesmunkát is. Az erő szót pedig szintén ezért tettem idézőjelbe, hiszen annak a térszerű három komponense így már nem csak a szokványos hármaserő a mozgást megfigyelő szerint, hanem az el van "rontva" a négyesmunkának megfelelő eltranszformálódott komponensekkel.) Ezek a mozgásegyenletek akkor is működnek természetesen, ha a nyomás negatív. így a negatív nyomás csak és kizárólag ezen az úton tud beilleszkedni a relativitáselméletbe, mivel a nyomás az mechanikai jellegű feszültség.

A Novobátzky könyvben a folytatás innentől hibás, ugyanis a következő lépésként a egyenletet használja fel, ami nem veszi figyelembe az állapotegyenlet szükséges létezését (és a negatív nyomás lehetőségét sem).

"A energiaimpulzus-tenzor divergenciája a téregyenletek miatt zérus.

.

Mivel , az utolsó tag . Tehát

.

Helyettesítsük -nek ezt a kifejezését (215)-be.

.

Az egyenletből , vagy ."

Ismét hiba, ráadásul elég súlyos. A divergenciák egyenlőségéből egyáltalán nem következik ilyen egyenlőség. , ahogy azt a legelején megtárgyaltam, általában nem szimmetrikus, és nem része négyestenzornak. A hibás lépések után végül az lett. egyértelműen az, pedig nem más, mint , ami szintén tenzor, és szimmetrikus is.

"Itt , és ezért végleges alakban

(216) .

A rugalmassági tenzor tényleg kifejezhető az energiaimpulzus-tenzorral."

Hát így biztos, hogy nem. A (216) végeredmény hibás, és a továbbiak is.